Il ricampionamento: teoria e pratica
Sei il visitatore numero
16482
Voglio ringraziare Jacopo e Giovanni Brembati, che hanno scritto questo interessante articolo dedicato al ridimensionamento delle immagini digitali.
Sul loro sito www.photoresampling.com propongono vari software, fra i quali spicca proprio un 'applicazione dedicata al ricampionamento, a mio avviso davvero molto efficace. Un punto di forza di questo software è certamente la possibilità di scegliere fra diversi metodi di ricampionamento, ma la vera peculiarità è la presenza di vari algoritmi proprietari sviluppati da Giovanni Brembati. Come vedremo nel corso dell'articolo, gli approcci per eseguire un ricampionamento sono diversi, e la loro efficienza dipende anche dall'immagine da elaborare, ma ciò che colpisce di più l'attenzione è il metodo GBLS , che lavora per iterazioni successive. Ci tenevo molto a sottolineare la qualità di questo software, sia perchè supera in qualità molti altri programmi più blasonati, ma anche perchè è completamente made in Italy.
1. Motivazione dell'articolo
Una foto la scattiamo per guardarla, a monitor o su carta. In ogni caso abbiamo la necessità di modificarne le dimensioni. Per modificare le dimensioni di un'immagine dobbiamo ricampionare.
Questo articolo vuole essere una breve introduzione al ricampionamento.
2. Origine del termine
Ricampionare significa campionare un'altra volta.
Una foto è il risultato di un campionamento della scena inquadrata. I pixel sono una rappresentazione non continua ma discreta della realtà.
Per ridimensionare un'immagine occorre ricostruire la scena originale, continua, e campionarla con una diversa frequenza.
3. Come ricostruire l'immagine originale
Introduciamo l'analisi in frequenza di un segnale.
In questo articolo segnale ed immagine vanno intesi come sinonimi.
In termini matematici, un'immagine è una funzione in due dimensioni g(x,y), che per ogni coordinata (x,y) fornisce un colore.
Se vogliamo rappresentare la nostra funzione nel dominio delle frequenze dobbiamo eseguire la trasformazione di Fourier.
La rappresentazione della funzione nel dominio delle frequenze viene detta: spettro della funzione .
Senza addentrarci troppo nella matematica,per capire come si comporta un'immagine nel dominio delle frequenze, possiamo dire che:
- un'alta frequenza corrisponde nel dominio spaziale ad una variazione significativa e repentina d'intensità (in un'immagine corrisponde ai dettagli)
- una bassa frequenza corrisponde nel dominio spaziale a zone di intensità quasi uniforme,la cui intensità varia lentamente
Per semplicità, consideriamo una sola dimensione x;quindi la nostra funzione è g(x).
Indichiamo con G(f) la rappresentazione della funzione g(x) nel dominio delle frequenze, e supponiamo che l'ampiezza spettrale sia rappresentata graficamente come nella figura seguente. fmax è la frequenza massima della funzione g(x).
|
Ampiezza spettrale
|
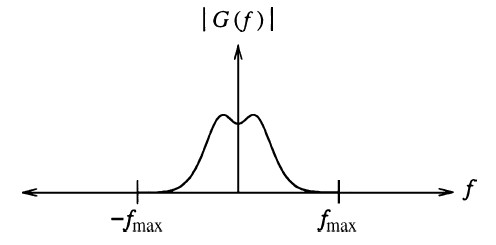 |
Se ora campioniamo g(x) con una frequenza fs otteniamo gs(x). Se eseguiamo la trasformazione di Fourier sulla gs(x) otteniamo Gs(f) il cui grafico è rappresentato nella figura successiva.
|
Ampiezza spettrale
|
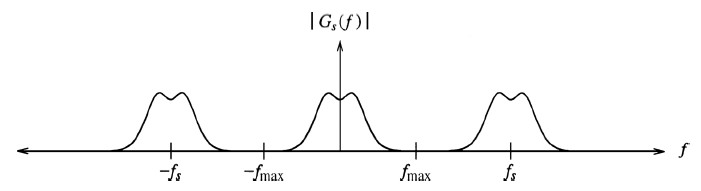 |
In base alle proprietà della trasformazione di Fourier risulta che lo spettro di una funzione campionata con frequenza fs è lo spettro originale replicato con periodo fs.
Dalla figura risulta evidente che per poter ricostruire lo spettro originale dobbiamo campionare con una frequenza sufficientemente grande da garantire la separazione delle repliche spettrali.
Se il campionamento è sufficientemente frequente, possiamo ricostruire lo spettro originale, e risalire alla funzione originale con una trasformazione inversa di Fourier.
D'atra parte, è evidente che se riduciamo la frequenza di campionamento le repliche spettrali vanno a sovrapporsi allo spettro originale inquinandolo irreversibilmente.
Tale sovrapposizione, denominata Aliasing, genera artefatti, e inibisce la possibilità di risalire allo spettro originale .
Ci siamo fatti un'idea di come vanno le cose ed ora possiamo enunciare il teorema del campionamento (Shannon 1949).
4. Il teorema del campionamento
Il teorema del campionamento afferma che un segnale è ricostruibile a partire da un suo campionamento se sono rispettate le seguenti condizioni:
il segnale ha un'ampiezza di banda limitata, cioè ha una frequenza massima finita
la frequenza di campionamento è superiore al doppio della frequenza massima presente nel segnale
La prima condizione assicura che è possibile fissare una frequenza di campionamento sufficientemente grande da tenere separate tra loro le repliche spettrali.
La seconda condizione stabilisce che la ricostruzione esatta del segnale continuo è possibile solo se la frequenza di campionamento fs è superiore al doppio della frequanza massima fmax.
La metà della frequenza di campionamento,fs/2, è la frequeza di Nyquist.
Abbiamo visto che il campionamento replica lo spettro del segnale e quindi se usiamo un filtro "a scatola" (box filter) H(f), siamo in grado di selezionare lo spettro originale.
|
Ampiezza spettrale
|
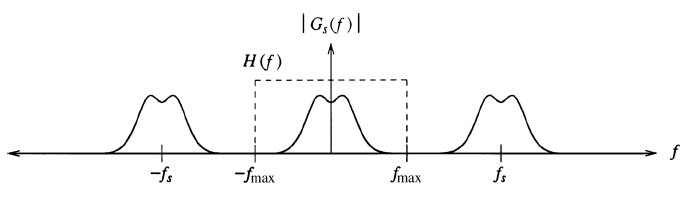 |
H(f) è un filtro passa-basso in grado di sopprimere tutte le componenti di frequenza superiore ad fmax.
Il filtro è ideale nel senso che fissa un punto di transizione tra la transmissione del segnale e la soppressione completa delle componenti in frequenza.
In un filtro reale non si ha un punto di transizione, ma una banda di transizione.
Per avere il filtro passa-basso nel dominio spaziale occorre operare la trasformazione inversa di Fourier della fuzione H(f).
Il risultato è la fuzione sinc.
|
Filtro passa-basso nel dominio spaziale
|
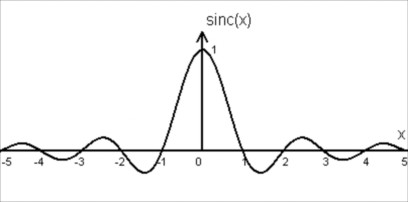 |
In base alle proprietà della trasformazione di Fourier: una moltiplicazione nel dominio delle frequenze corrisponde ad una convoluzione nel dominio spaziale.
Quindi, per ricostruire il segnale originale, dobbiamo eseguire una convoluzione del segnale campionato con la funzione sinc.
5. Dalla teoria alla pratica
Cominciamo ad analizzare se una foto può essere considerata il risultato di un buon campionamento.
Come abbiamo visto, il teorema del campionamento impone che il segnale abbia un'ampiezza di banda limitata e che la frequenza di campionamento sia superiore al doppio della frequenza massima.
Sappiamo che le fotocamere utilizzano un filtro AA (Anti-Aliasing).
Quindi il produttore si è preoccupato di predisporre un filtro passa-basso che tagli le frequenze incompatibili con la periodicità dei fotoricettori.
Possiamo affermare che per le nostre foto esiste la possibilità teorica di ricostruire il segnale originale .
Se vi state preoccupando per la presenza del termine teorica , fate bene. Vediamo perchè.
Torniamo alla funzione che ci permette di ricostruire il segnale originale, la funzione sinc.
Questa funzione non è limitata. Questo significa che, per ricostruire ogni singolo punto dell'immagine, avremmo bisogno di considerare un intorno di campioni, i nostri pixel, infinito.
La ricostruzione ideale non è praticabile .
Per approssimare la funzione sinc e contenere i tempi di elaborazione, possiamo troncarla non troppo lontano dall'origine.Di solito, in due dimensioni, si fissa una finestra 5x5 o 7x7.
Per troncare la funzione usiamo un filtro a scatola (filter box), come nella figura seguente.Il filtro è evidenziato in rosso.
|
Filtro passa-basso nel dominio spaziale
|
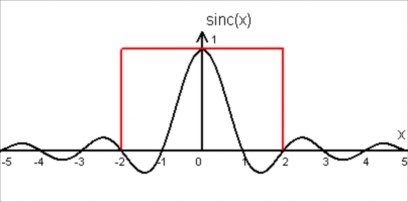 |
Quando però tronchiamo la funzione sinc si manifestano aloni intorno a zone in cui l'intensità varia rapidamente e sostanzialmente (edge). Questo effetto è noto come fenomeno di Gibbs.
Sono state proposte diverse funzioni sostitutive del filtro a scatola che potessero modulare la funzione sinc attenuando il fenomeno di Gibbs:
Lanczos
Welch
Hann
Hamming
Blackman
Parzen
Kaiser
Dato che attualmente Lanczos e Welch sono presenti in PhotoResampling, vediamo quali risultati producono.
| Immagine originale |
 |
|
Ricampionamento Lanczos
300%
|
 |
|
Ricampionamento Welch
300%
|
 |
Il filtro di Welch produce un'immagine leggermente più contrastata che genera una sensazione di maggior nitidezza.
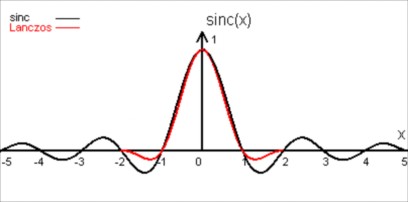
Esaminiamo i due filtri utilizzati :
|
Filtro di Lanczos
|
Filtro di Welch
|
 |
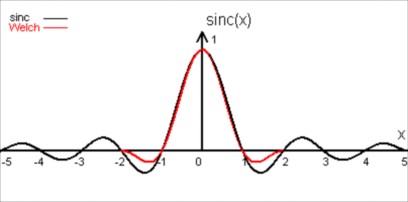 |
Notiamo che l'ampio lobo positivo centrale ha un andamento pressocchè identico e che i due lobi negativi in Welch sono un po' più profondi.
Quindi abbiamo capito che i lobi negativi tendono a produrre un risultato più nitido, fino a sfociare negli aloni pronunciati della sinc troncata.
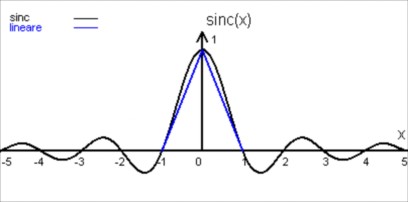
6. Metodo di interpolazione bilineare
L'interpolazione lineare consiste nel supporre che il colore vari linearmente tra un pixel e l'altro.
Il termine bilineare discende dal fatto che si interpola linearmente due volte. La prima volta orizzontalmente e la seconda verticalmente, o viceversa.
Vediamo il risultato dell'interpolazione bilineare.
Attenzione,il filtro triangolare va a sostuire la funzione sinc. Non è un filtro da applicare alla funzione sinc,come in Lanczos o Welch.
L'andamento della funzione lineare viene rappresentato insieme alla funzione sinc solo ai fini di valutarne le differenze.
|
Filtro lineare
|
|
|
Ricampionamento bilineare
300%
|
 |
I lobi negativi,presenti nella funzione sinc, sono stati tagliati via e di conseguenza il risultato non è molto nitido.
Il lobo positivo viene approssimato in maniera un po' grossolana.
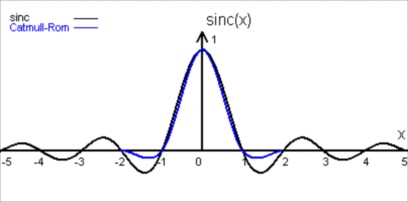
7. Metodi di interpolazione bicubica
Avendo visto che una funzione lineare si discosta abbastanza dalla funzione sinc, è naturale pensare che una funzione di grado superiore possa produrre una migliore approssimazione.
Una funzione cubica offre un buon compromesso tra qualità e complessità.
Naturalmente è possibile definire un gran numero di curve di terzo grado che approssimino la funzione sinc.
Vediamone alcune.
Attenzione,le cubiche vanno a sostuire la funzione sinc. Non sono filtri da applicare alla funzione sinc,come in Lanczos o Welch.
L'andamento delle cubiche viene rappresentato insieme alla funzione sinc solo ai fini di valutarne le differenze.
|
Cubica Catmull-Rom
|
|
|
Ricampionamento Catmull-Rom
300%
|
 |
La cubica di Catmull-Rom è matematicamente, e forse anche visivamente, la migliore cubica.
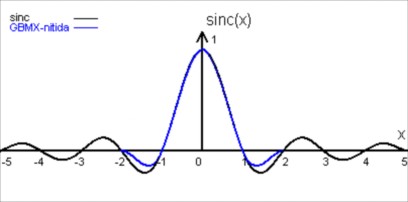
Ora vediamo una cubica molto nitida.Questa curva è presente in PhotoResampling. Il metodo di interpolazione GBMX copre una serie di bicubiche che producono risultati più o meno nitidi.
|
Cubica GBMX-nitida
|
|
|
Ricampionamento GBMX-nitida
300%
|
 |
Come potete vedere i lobi negativi sono più pronunciati di quelli presenti in Catmull-Rom.
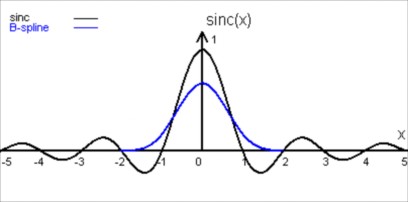
Concludiamo la nostra carrellata con una cubica che produce risultati piuttosto sfocati : B-spline.
|
Cubica B-spline
|
|
|
Ricampionamento B-spline
300%
|
 |
Come potete vedere non abbiamo più i lobi negativi.
8. Alcune considerazioni aggiuntive
Fin qui abbiamo cercato di ricostruire l'immagine originale senza alcuna considerazione sulle sue caratteristiche. Sappiamo però, per esempio, che il sistema visuale umano è molto sensibile alla qualità delle variazioni di intensità (gli edge).
In Photoresampling, tale tema è stato approfondito ed ha portato alla creazione del metodo iterativo GBLS.
|
Ricampionamento GBLS (2 iterazioni) del 300%
|
 |
Come potete vedere le venature sulle ali sono ben delineate e l'immagine ha una buona nitidezza.
9. Aliasing in azione
Finora abbiamo parlato sempre di ingrandire un'immagine. Vediamo cosa succede se decidiamo di ridurne sensiblimente le dimensioni.
|
Immagine originale
|
 |
|
Immagine ricampionata al 40%
|
 |
Decisamente bruttina. Cosa è successo?
Non abbiamo tenuto conto del teorema del campionamento.Gli artefatti che vediamo sono l'aliasing prodotto dalla sovrapposizione delle repliche spaziali sullo spettro dell'immagine originale.
Il teorema del campionamento ci suggerisce cosa dobbiamo fare: prima di ricampionare, dobbiamo applicare un filtro passa-basso in modo da ridurre la frequenza massima del segnale.
Anche se esistono filtri passa-basso migliori, applichiamo un semplice filtro gaussiano all'immagine:
|
Immagine filtrata
|
 |
Ed ora ricampioniamo:
|
Immagine filtrata ricampionata al 40%
|
 |
Va decisamente meglio. Se vogliamo, possiamo aumentare un po' la nitidezza.
Un'ultima verifica del teorema del campionamento: proviamo a riportare l'immagine ottenuta alle dimensioni originali:
|
Immagine filtrata ricampionata al 40% ricampionata al 250 %
|
 |
Il risultato è abbastanza simile all'immagine filtrata che, per il ricampionamento, è da considerarsi l'immagine originale.
Abbiano ottenuto una buona ricostruzione dell'immagine originale.
10. Conclusione
La ricostruzione perfetta dell'immagine originale non è possibile. Il ricampionamento produce sempre un'immagine degradata.
- Utilizzando algoritmi diversi si ottengono risultati diversi.
- Non esiste un algoritmo migliore in assoluto e quindi la scelta va indirizzata in base all'immagine specifica che vogliamo ridimensionare.
- Considerando le proprietà della visione umana è possibile ottenere immagini più gradevoli.
- Se si ha l'esigenza di ridurre significativamente le dimensioni di un'immagine, dobbiamo prima eliminare le alte frequenze utilizzando un filtro passa-basso.
Se vuoi parlare con noi di questo articolo vieni a trovarci sul FORUM
E' vietata la riproduzione anche parziale di questo articolo senza il consenso dell'autore.
|