|
Sei il visitatore numero 36625
Introduzione In questo articolo, che conclude la serie sulle tecniche di photo stitching pubblicata su PhotoActivity, approfondiremo la teoria relativa al concetto di “nitidezza” di una stampa fotografica, per poi mostrare come le attuali tecnologie digitali possono aiutarci ad incrementarla. Come sottolineato nel primo articolo, l’approccio del “tutto nitido” non rappresenta necessariamente la ricetta magica per ottenere immagini più apprezzabili, anzi molto spesso una sapiente composizione di aree nitide ed aree sfocate rappresenta un elemento estremamente gradevole nella composizione di un’immagine fotografica. Tuttavia è innegabile che esistono situazioni nelle quali la nitidezza dei vari piani costituisce un fattore decisivo, come spesso accade per la stampe “Fine-Art” relative ad immagini di paesaggio. Revisione del 1 Novembre 2007: Scisso in più paragrafi l'ex paragrafo 5 (con conseguenti riadattamenti ). Aggiunto il paragrafo 6, relativo alla teoria del campionamento digitale di una immagine.
01 - Il concetto di "nitidezza" secondo il sistema di visione umano
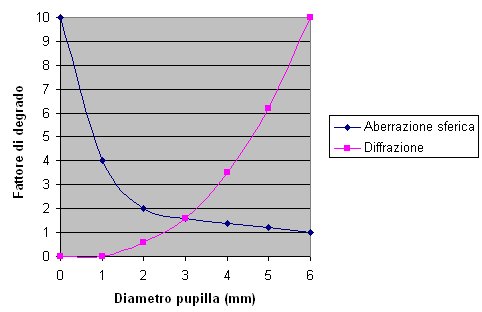
Prima di affrontare il problema dal punto di vista operativo, è necessario chiarire cosa si intende con il termine “nitidezza”: per fare ciò occorre fornire qualche elemento di conoscenza riguardante il sistema di visione umano. L'occhio umano può essere equiparato ad un sistema ottico, pertanto è possibile analizzarne le prestazioni applicando le classiche leggi dell'ottica geometrica. Ovviamente non è questa la sede più adatta per approfondire nel merito questi complessi temi, ma puntiamo direttamente la nostra attenzione sui due limiti principali del sistema: - aberrazione sferica assiale: è un difetto ottico per il quale i raggi luminosi che penetrano dalla zona periferica della pupilla si focalizzano su un piano diverso rispetto ai raggi che penetrano lungo l’asse ottico. L’entità di questa aberrazione decresce col decrescere del diametro della pupilla (di fatto paragonabile all’apertura del diaframma) - diffrazione ottica: è un difetto dovuto alla propagazione ondulatoria della radiazione luminosa. I raggi luminosi tendono infatti a deviare il loro percorso quando transitano molto vicino a soggetti opachi, nel nostro caso il bordo della pupilla. Il degrado qualitativo dovuto alla diffrazione decresce incrementando il diametro della pupilla. In buona sostanza i due difetti non possono essere eliminati contemporaneamente: la condizione qualitativamente migliore deriva dunque da un compromesso, che corrisponde al punto in cui le due curve di degrado (aberrazione sferica e diffrazione) si intersecano:
Come si vede, i due difetti ottici raggiungono il minimo comune in corrispondenza di un diametro pupilla di circa 3mm: questa è dunque l’apertura pupillare più favorevole in termini di acutezza visiva. L'illuminazione ambientale gioca quindi un ruolo decisivo, perché determina l'apertura pupillare: in pratica il nostro cervello regola l'apertura momento per momento, con una sorta “esposizione automatica”. Il seguente grafico riassume i valori medi di apertura pupillare, ottenuti verificando su vari individui le reazioni della pupilla al variare dell’illuminazione ambientale (valori approssimati, espressi in Lux con scala logaritmica) :
Dal grafico risulta evidente il ruolo dell’illuminazione della scena: per raggiungere la massima acutezza visiva, in corrispondenza del diametro pupilla di 3mm, abbiamo bisogno di circa 2500 Lux, che corrispondono a circa 10 EV (l'equivalente di ISO100, f/2.8 1/60sec). Giunti a questo punto non rimane che quantificare la risoluzione dell’occhio, ovviamente per via sperimentale.
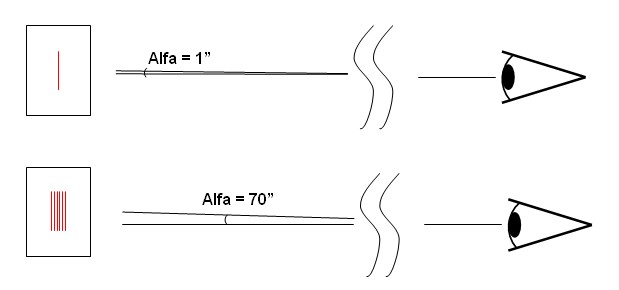
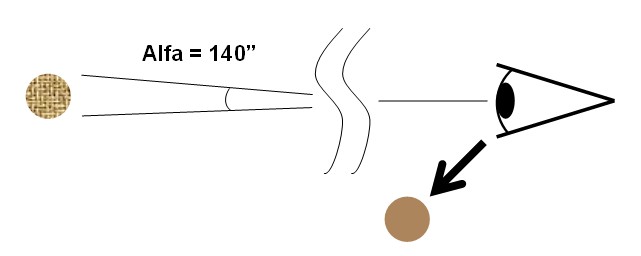
In realtà la risoluzione corrispondente ad Alfa=70” si ottiene solo con soggetti ad altissimo contrasto (ad esempio linee nere su sfondo bianco, ben illuminato), mentre in condizioni di contrasto medio-alto, come accade per la maggior parte dei soggetti che ci circondano, la risoluzione effettiva si dimezza, con Alfa che assume un valore attorno ai 140”(circa due primi d’arco): per le applicazioni fotografiche è questo il valore che possiamo prendere come riferimento. E' tuttavia importante sottolineare un paio di aspetti: - i 140" rappresentano un valore medio, riferito ad individui normovedenti - in alcuni casi il valore preso a riferimento è diverso -in una fascia compresa tra i 120” ed i 170”- perché si fissano arbitrariamente situazioni di misura diverse, con particolare riferimento al contrasto dei soggetti ed alle condizioni di illuminazione. Una acutezza visiva di circa 140" implica che l’unità di spazio minima che siamo capaci di distinguere è di 68mm a 100 metri di distanza dal soggetto, 6.8mm a 10 metri, 0.68mm ad 1 metro, e così via.
Questa unità di spazio minima, geometricamente definibile come diametro del cerchio descritto dalla proiezione del cono visivo Alfa, è chiamata comunemente “Circolo di Confusione” (CdC), e si definisce matematicamente nel seguente modo: CdC = D * 2 * tan (Alfa / 2) Dove: Fissiamo adesso alcuni valori standard: - la risoluzione dell’occhio Alfa =140", dunque l'espressione 2 * tan(Alfa/2) diviene una costante di valore 0,00068 Pertanto: CdC = Df * 0,00068 L'espressione è adesso molto semplificata: risulta evidente come il CdC ammesso dipenda esclusivamente dalla diagonale Df del formato dell'immagine. Di conseguenza, per conoscere qual'è il valore di CdC ammissibile in ripresa (ovvero sul sensore), si applica dunque la stessa formula considerando un valore Df pari alla diagonale del sensore. Questi sono i valori del CdC sensore che si ottengono per i più comuni formati di ripresa:
Ecco allora il concetto fondamentale: premesso l'utilizzo dei valori standard sopra indicati, tutto ciò che viene registrato dal sensore all’interno del Circolo di Confusione, indipendentemente dalla nitidezza effettiva, non è riconoscibile sulla stampa finale e l’area viene rilevata dall’occhio come un singolo punto nitido.
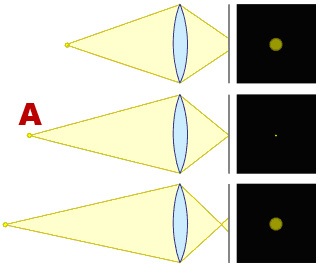
Entro questo CdC potremo allora trascurare perdite di qualità dovute ad aberrazioni ottiche, diffrazione ed imprecisioni di messa a fuoco: proprio da questa tolleranza nasce il concetto di “Profondità di Campo” che andiamo ad analizzare nel prossimo paragrafo. Un punto “A” (di diametro nullo) sul quale abbiamo perfettamente impostato la messa a fuoco viene virtualmente restituito come un punto (anch’esso di diametro nullo) sul sensore della nostra fotocamera digitale.
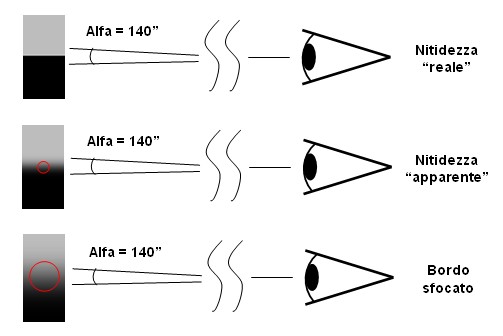
Dato che –come visto in precedenza- la risoluzione del sistema visivo umano ha un limite, i circoli sfumati potranno essere percepiti come tali solo se il loro diametro supera la dimensione del Circolo di Confusione ammesso per il sensore utilizzato in ripresa. Si determina così il concetto di “nitidezza apparente” in contrapposizione alla ”nitidezza reale”, che si ottiene esclusivamente sull'area dell'immagine che risiede sul piano di messa a fuoco.
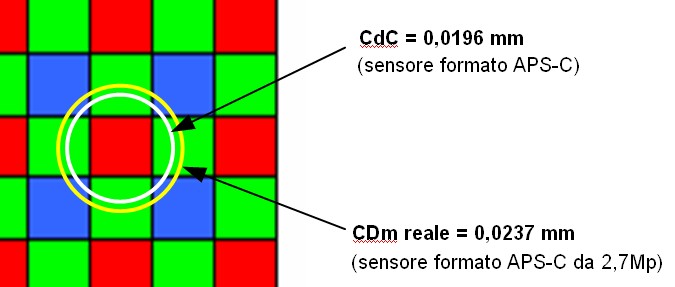
L’immagine seguente riassume schematicamente questi concetti, considerando a titolo di esempio la visione di un bordo a medio contrasto, riprodotto prima in versione ideale e successivamente con due livelli di sfumatura. Nei primi due casi l’occhio percepisce un bordo nitido, mentre nell’ultimo caso percepisce un bordo sfumato, perchè i punti che compongono il bordo raggiungono una sfumatura (circolo rosso) di diametro superiore al CdC ammesso.
Come conseguenza di questo comportamento, si determina il principio di “Profondità di campo” PdC, ovvero una fascia di spazio davanti alla fotocamera nella quale gli oggetti presenti saranno riprodotti in stampa entro il limite di "nitidezza apparente". limite anteriore = D / (1 + CdC * fn * ((D - F) / F 2 )) limite posteriore = D / (1 - CdC * fn * ((D - F) / F 2 )) dove: D = Distanza del soggetto messo a fuoco, misurata dal piano del sensore (mm) E’ interessante notare che, a parità di condizioni di ripresa (obiettivo, apertura, distanza di messa a fuoco), la dimensione del Circolo di Confusione risulta determinante per stabilire l'estensione della profondità di campo. Il rispetto dei CdC riportati in precedenza (relativi ai vari formati di sensore) ci consente come detto di ottenere stampe visionabili da una distanza “standard” pari alla diagonale del formato. Chiarito il ruolo decisivo della scelta del CdC, non resta che comprendere come possiamo gestirlo in fase di scatto. Ebbene, a parità di regolazione della messa a fuoco, il grado di sfumatura dei circoli può essere significativamente ridotto solo riducendo l’apertura del diaframma (incremento del numero f/ ). I riferimenti della profondità di campo sono spesso riportati sui barilotti delle ottiche, soprattutto su quelle a focale fissa. Nel seguente caso si imposta la messa a fuoco sulla “distanza iperfocale" Dh per ottenere la massima estensione di PdC che comprenda anche l'infinito:
In questo caso la distanza iperfocale utilizzata è circa 4mt: impostando diaframma f/22 si ottiene una Pdc estesa da circa 2 metri all'infinito. Le tacche di colore arancio sul barilotto mostrano in maniera intuitiva la PdC ottenibile a f/22, valore di diaframma riportato in arancio sulla ghiera dei diaframmi. La distanza iperfocale può essere individuata anche per via matematica, applicando la seguente formula: Dh = F ² / (CdC * fn) dove: F = lunghezza focale dell'ottica utilizzata in mm (esempio: 50) Nel nostro caso la formula conferma pienamente le indicazioni riportate sul barilotto: Distanza iperfocale = 50 ² / (0,0294 * 22) = 3865mm ovvero 3,86 metri
Bisogna tuttavia prestare molta attenzione alle indicazioni presenti sui barilotti delle ottiche progettate per il formato 35mm, perché si riferiscono ovviamente al CdC del formato 35mm (full-frame). Molte D-reflex montano invece sensori formato APS-C dove –come visto- il CdC ammesso è decisamente minore. Ebbene, applicando le relazioni matematiche esposte in precedenza, si può dedurre che per ottenere il CdC standard sui sensori APS-C, si deve chiudere il diaframma di 1 stop in più rispetto a quanto indicato dai riferimenti di PdC presenti sul barilotto. Nell'esempio precedentemente illustrato non si possono dunque utilizzare i riferimenti rossi (f/22) perché si dovrebbe poi chiudere a f/32 (non disponibile). La massima PdC ottenibile è dunque quella indicata dai riferimenti di colore blu (f/16), chiudendo il diaframma a f/22. La PdC sui formati APS-C sembrerebbe dunque inferiore rispetto a quella ottenibile sul formato 35mm, ma tenendo conto che la "focale equivalente" è 1,5 volte maggiore, in realtà è proprio l’APS-C ad avere una maggior profondità di campo disponibile. In linea generale, a parità di diaframma la profondità di campo aumenta col decrescere del formato del sensore. Dopo aver analizzato come si gestisce la profondità di campo, è opportuno ricordare che l'utilizzo di un diaframma molto chiuso comporta uno scadimento qualitativo dovuto alla diffrazione: si incrementa infatti la percentuale di luce che, transitando in prossimità delle lamelle del diaframma, flette il proprio percorso. Per le ottiche progettate per i formati 35mm e APS-C (16x24mm) il limite si trova generalmente attorno ad f/8-f/11: diaframmando ulteriormente non si ottiene un miglioramento delle prestazioni bensì un graduale decadimento (vedere ad esempio il test del Nikkor 105mm).
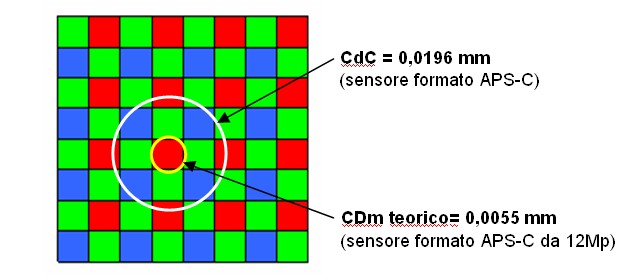
Dall’esposizione sin qui fatta abbiamo compreso che, al fine di ottenere una stampa di buona “nitidezza apparente”, l’effetto combinato delle aberrazioni ottiche, della diffrazione e del fuori fuoco su un punto non deve eccedere il CdC ammesso per il formato del sensore in uso. Nella nostra esperienza di tutti i giorni esiste il concetto che, proprio a causa del limite di acutezza della visione umana, per ottenere maggior dettaglio di un oggetto ci avviciniamo ad esso. Eseguiamo questa operazione in modo automatico, senza neanche rendersene conto. Spesso facciamo la stessa cosa anche con le stampe fotografiche, ma l’utilizzo di “nitidezza apparente” di fatto non fornisce ulteriori informazioni, e questo provoca talvolta una sensazione negativa. La “necessità” di ulteriori dettagli è certamente un elemento soggettivo, dipende anche dalla tipologia e dalle dimensioni dell’immagine che stiamo osservando. Soprattutto le stampe che raffigurano elementi imponenti (ad esempio paesaggi) si prestano molto ad un esame ravvicinato, per un effetto che definirei di “immersione fotografica”. Ebbene, in questi casi può essere utile ridurre più possibile il CdC in fase di ripresa, utilizzando uno dei seguenti metodi: - maggiore chiusura del diaframma. Questo metodo –come detto- trova un serio limite da f/11 in poi, dove la diffrazione determina un progressivo scadimento della qualità dell'immagine. - utilizzo di ottiche di tipo Tilt/Shift, che permettono di orientare il piano della “nitidezza reale” grazie all’applicazione della regola di Scheimpflug. Si tratta tuttavia di dotarsi di attrezzature particolari (e relativamente costose) con le quali si ottengono normalmente buoni risultati, ma non in alcune situazioni di ripresa (vedi il primo articolo). - realizzazione del “Focus stitch”, con il quale si realizzano più scatti della stessa scena, impostando per ciascuno scatto una diversa messa a fuoco; successivamente si selezionano le aree più nitide di ciascuno scatto in post-produzione digitale. Quest’ultimo è il metodo che ci apprestiamo ad esaminare in maniera approfondita. Prima di entrare nel merito della tecnica del Focus Stitch, bisogna chiarire come si determina la minima distanza dalla quale si può osservare una stampa senza ottenere un effetto di insufficiente nitidezza. A tal fine occorre valutare la risoluzione effettiva del sistema obiettivo-sensore, tenendo presente che in ambito digitale le differenze di potere risolvente tra sensori diversi, a parità di formato e di sensibilità ISO nominale, possono essere molto più elevate che in ambito analogico. Basti pensare che non più di 4 anni fa erano ancora in produzione fotocamere formato APS-C con appena 2,7Mpixel, mentre oggi sullo stesso formato troviamo alloggiati oltre 12Mpixel. L’unità minima di registrazione del sensore è certamente il singolo pixel, pertanto possiamo esprimere la risoluzione del sensore come “Circolo di Dettaglio minimo” CDm: CDm = (Lmm / Lpix) dove: Facciamo un esempio pratico utilizzando un sensore di formato APS-C da 12Mpixel (4288x2848): CDm = 23,7 / 4288 = 0,0055 mm
In realtà il valore CDm ottenuto è da considerarsi un valore teorico, perché nella realtà si deve tener conto di problemi dovuti alle proprietà sia del sensore che dell'obiettivo utilizzato. Per ciò che riguarda il sensore, i principali limiti sono dovuti a: - distribuzione dei pixel RGB secondo la matrice di Bayer: di fatto in ciascuna cella elementare (pixel) viene registrato un solo colore primario, dunque per ricostruire il valore degli altri due colori primari è necessario un sofisticato processo di elaborazione chiamato "demosaicizzazione" (vedi articolo DCRAW). - filtro ottico anti-alias: una azione eccessiva di questo filtro posto davanti al sensore, può provocare una ulteriore diminuzione del potere risolvente (vedi più avanti). Questi due fattori, ovviamente oltre alla densità dei pixel, determinano la risoluzione effettiva del sensore (Sr). Per ciò che riguarda invece l'obiettivo, la risoluzione effettiva (Lr) è limitata dalle aberrazioni ottiche (in maggior misura nella periferia del fotogramma) e dalla diffrazione (con valori alti di f/ rispetto al formato in uso).
Abbiamo appena visto che obiettivo e sensore posseggono un proprio potere risolvente. La condizione ideale sarebbe certamente disporre di un sensore con risoluzione sufficiente a catturare tutto il dettaglio trasmesso dai migliori obiettivi in commercio. Qual'è il corretto rapporto tra le due risoluzioni, al fine di raggiungere questa condizione ideale? Il teorema del campionamento dimostra che è possibile ricostruire correttamente un segnale analogico, a patto che la frequenza di campionamento Fs sia almeno doppia della massima frequenza contenuta nel campione stesso. Fs = 2 * Fmax In una mira ottica, la sequenza di righe parallele bianche e nere alternate può essere definita come una frequenza spaziale ad onda quadra, la quale, in accordo con l'analisi di Fourier, è costituita dalla somma di infinite onde armoniche sinusoidali di frequenza crescente: il passaggio repentino dal nero al bianco (e viceversa) sarebbe pertanto ricostruibile solo con un campionamento a frequenza Fs infinita (in pratica con una densità infinita di pixel sul sensore).
Tuttavia le aberrazioni e/o la diffrazione introdotte dall'obiettivo costituiscono un vero e proprio filtro ottico passa-basso, che taglia via gran parte delle frequenze spaziali più elevate: si rende così possibile l'utilizzo di frequenze di campionamento Fs (ovvero densità di pixel) più contenute. Se tuttavia la frequenza di campionamento Fs del sensore non raggiunge il valore richiesto dal teorema, nasce l'esigenza di installare un particolare vetro ottico davanti al sensore (chiamato filtro anti-alias), calcolato in modo attenuare le frequenze spaziali superiori al doppio della frequenza di campionamento del sensore (parametro noto ai costruttori). Se questo filtro è assente oppure ha un azione insufficiente, il potere risolvente del sistema obiettivo-sensore risulta maggiore, ma la ricostruzione del segnale può risultare disturbata, provocando l'insorgere di fastidiosi difetti come il Moirè (riproduzione di trame non presenti nella realtà). I migliori sensori attualmente in commercio (12Mp su formato DX, 21Mp su formato 35mm), seppur capaci di catturare gran parte delle informazioni trasmesse dalle ottiche più performanti, non riescono a rispettare pienamente il teorema del campionamento.
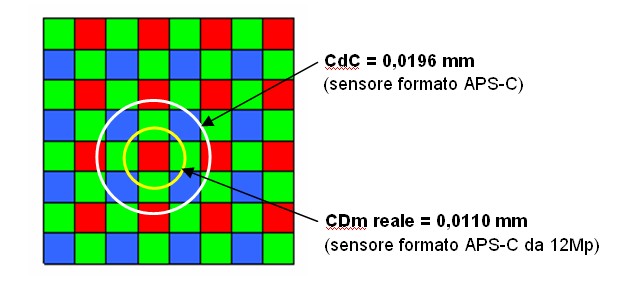
Dopo aver analizzato le problematiche legate alla riproduzione digitale di una immagine, cerchiamo di quantificare il valore del circolo di dettaglio minimo CDm reale. Seguendo la via sperimentale, si può utilizzare la metologia proposta da Imatest ; all'interno del sito web si trova il software necessario ed una accurata descrizione delle condizioni necessarie per i test. E' inoltre presente un’ampia documentazione teorica (solo in lingua inglese, purtroppo). Nella seguente immagine è rappresentata una mira originale (sequenza di linee parallele, con spaziatura decrescente) ed un esempio di come la mira stessa viene riprodotta da un sistema obiettivo-sensore:
I parametri da prendere in esame sono essenzialmente due: - LW/PH è il numero di linee parallele riproducibili sfruttando il lato corto del sensore Contrariamente a quanto si potrebbe pensare, la nitidezza percepita non si misura sul massimo LW/PH ottenibile (dove il MTF è molto basso, con linee appena riconoscibili), bensì sul valore LW/PH per il quale il MTF risulta il 50% del suo valore massimo (MTF50). Il risultato medio dei test indica che, utilizzando ottiche di alta qualità progettate per il formato 35mm, si ottiene una risoluzione media del sistema a MTF50 intorno al 60%-70% del numero di pixel presenti sull’asse. In virtù di ciò si deve introdurre un fattore di degrado del CDm teorico, il cui valore minimo può essere considerato 1,7 ma, volendo considerare un valore che riassuma il comportamento medio dell’ottica (media tra centro e bordi del fotogramma), si può considerare un valore medio di 2. Si ottiene cioè un valore del CDm reale pari al doppio del lato del singolo pixel. Nel nostro esempio otterremo perciò: CDm reale = CDm * 2 = 0,0110 mm
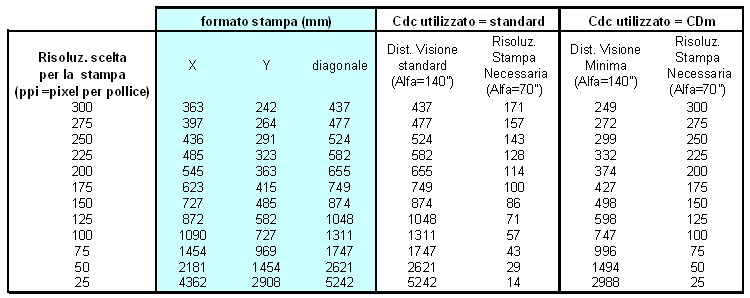
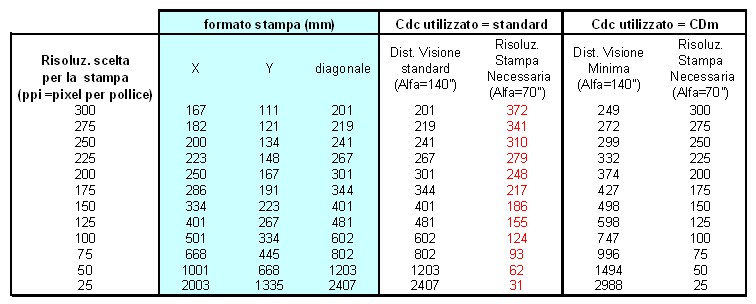
DVm = (CDm reale / CdC) * D Nel nostro caso: DVm = (0,0110 / 0,0196) * D = 0,56 * D Pertanto si può concludere che: - rispettando in fase di ripresa il valore di CdC standard, la stampa potrà essere osservata da una distanza pari a D, ovvero la diagonale del formato - utilizzando in fase di ripresa un valore di CdC pari a CDm reale, la stampa potrà essere osservata da una distanza minore (pari al 56% di D) senza notare alcun degrado. La seguente tabella riassume le caratteristiche delle stampe riproducibili con una stampante capace di 300 dpi (punti per pollice), utilizzando il pieno fotogramma della fotocamera APS-C da 12Mp, in funzione della scelta dei ppi (pixel per pollice in stampa) e del CdC utilizzato in fase di ripresa:
Nelle colonne “Risoluz. Stampa Necessaria” è indicata la risoluzione di stampa necessaria (ppi) calcolata in base alla risoluzione massima dell’occhio (alfa=70”), relativamente alla distanza di visione: questo valore di risoluzione deve essere minore o uguale alla risoluzione scelta (prima colonna). Nella condizione più favorevole troviamo la stampa eseguita utilizzando 300 pixel per pollice in stampa (dimensione 24x36cm), che potrà essere visionata da 43cm di distanza nel caso di CdC standard oppure da 25 nel caso di CdC=Cdm reale.
Abbiamo appena visto le potenzialità di un sensore APS-C da 12Mpixel, uno dei più performanti tra quelli attualmente sul mercato, ma è altresì interessante evidenziare i limiti che si incontrano utilizzando sensori con un numero di pixel inferiore. Ad esempio, poniamo il caso limite di un sensore formato APS-C da 2,7 Mpixel (2000x1312): CDm = 23,7 / 2000 = 0,0118 mm CDm reale = CDm * 2 = 0,0237 mm
Ebbene, in questo caso il CDm risulta addirittura superiore al CdC ammesso per il formato, per cui la regola della distanza di visione standard non trova applicazione: la minima distanza di visone risulta infatti del 21% superiore a quella “standard”: Dvm = (0,0237 / 0,0196) * D = 1,21 * D Di seguito è riportata la tabella delle caratteristiche delle stampe riproducibili con una stampante capace di 300 dpi (punti per pollice), relativa a questo sensore:
La colonna di colore rosso avverte che la risoluzione di stampa necessaria (ppi) per la distanza di visione “standard” è sistematicamente insufficiente rispetto a quella scelta per la stampa: di fatto non andrebbe utilizzato il CdC standard, bensì il CDm reale, che comporta una distanza di visione incrementata del 21%. Nel confronto con la precedente tabella si nota che un minor numero di pixel comporta, a parità di ppi scelti, una stampa necessariamente più piccola. Questo vale ovviamente anche nel caso si effettuino ritagli dell’immagine originale. La scelta dei parametri di scatto (compreso il tipo fotocamera) deve essere finalizzata esclusivamente alle condizioni di visione della stampa previste. Ad esempio, i grandi cartelloni pubblicitari non provengono da stitch gigapixel, bensì da singoli scatti eseguiti con normali fotocamere: questo perché si accetta una distanza di visione minima nell’ordine dei metri o addirittura delle decine di metri. Il Focus stitch, nelle situazioni di ripresa che lo rendono applicabile, permette di fissare la dimensione del CdC virtualmente per qualsiasi profondità di campo necessaria, pertanto si rivela un ottimo strumento per ridurre la minima distanza di visione delle stampe. La condizione necessaria per sfruttare al massimo le potenzialità del Focus stitch è quella di utilizzare un sensore il cui CDm reale (Circolo di Dettaglio minimo) è significativamente inferiore al CdC (Circolo di Confusione) ammesso per il formato, in modo da sfruttare al massimo il potere risolvente dell'ottica utilizzata. Tuttavia il Focus Stitch è utilizzabile con successo anche quando si ritiene sufficiente il CdC standard, ma si vuole estendere la profondità di campo oltre i limiti imposti dal CdC stesso. Per eseguire gli scatti di test, ho utilizzato una fotocamera con sensore da 10Mpixel con un'ottica fissa di focale 50mm. Gli scatti sono stati eseguiti nelle massime condizioni di stabilità della fotocamera, ed il particolare della scena che ho utilizzato come riferimento è di tipo statico. La post-produzione si è limitata alla conversione del RAW, applicando in CameraRaw un valore di maschera di contrasto uguale per tutti gli scatti, pari a 25.
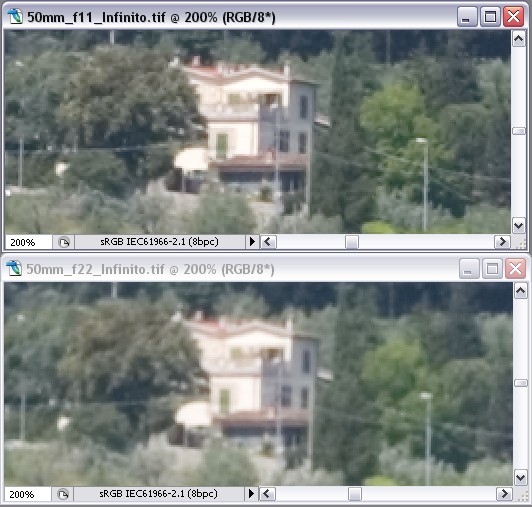
Di questa immagine ho inizialmente eseguito due scatti con messa a fuoco su infinito: la prima con diaframma f/11, l'altra con f/22. Questi i risultati, mostrati con dettaglio al 200%:
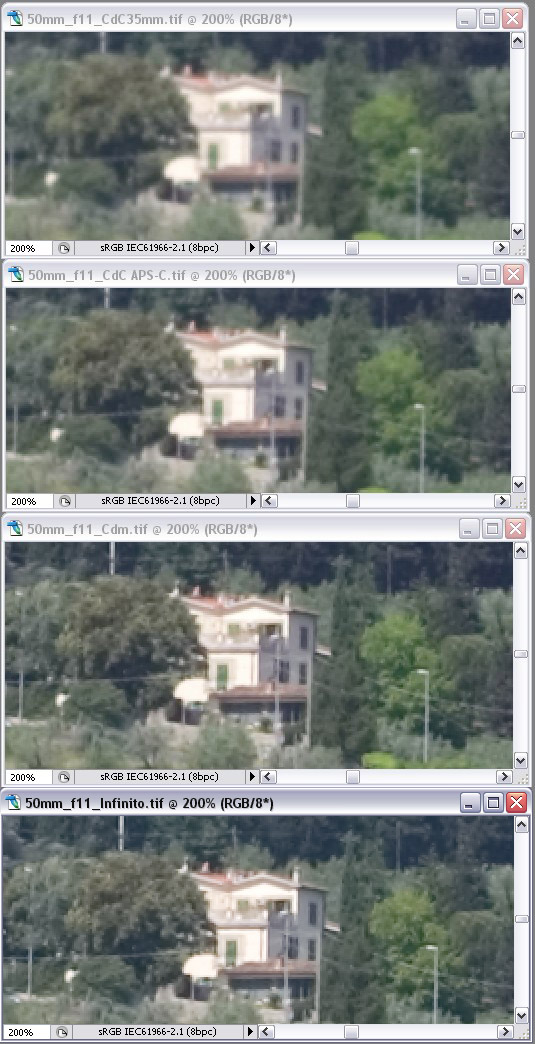
Nello scatto a f/22 si nota chiaramente il degrado dovuto alla diffrazione. Per una miglior valutazione dei risultati, il test dell’impatto del CdC sulla nitidezza sarà dunque effettuato sul diaframma f/11. A questo proposito ho realizzato una serie 4 di scatti con diversa messa a fuoco: 1- iperfocale calcolata con il Cdc del formato 35mm (0,0294mm): sul barilotto si allinea al simbolo dell'infinito la tacca Pdc relativa al diaframma utilizzato; 2- iperfocale calcolata con il Cdc del formato APS-C (0,0196mm): sul barilotto si allinea al simbolo dell'infinito la tacca Pdc relativa ad un f/stop in meno rispetto al diaframma utilizzato (ad esempio per f/22 si utilizza la tacca f/16); 3- iperfocale calcolata con il Cdc pari al CDm reale. Per il nostro sensore da 10Mp i calcoli indicano CDm teorico =0,006, mentre il fattore di degrado è stato considerato pari a 2. Pertanto il CDm reale risulta di 0,012mm e la distanza iperfocale per ottenerlo risulta di circa 18mt. In questo caso si può utilizzare con buona approssimazione la tacca Pdc relativa a due f/stop in meno rispetto al diaframma utilizzato (se disponibile); 4-messa a fuoco su infinito (condizione di riferimento) Questi i risultati, mostrati con dettaglio al 200% :
Valutiamo le differenze qualitative tra i vari scatti: - lo scatto con iperfocale calcolata sul CdC del formato 35mm ha –come da previsioni- la nitidezza minore: una stampa generata da questo file rivelerebbe questa minor nitidezza da una distanza di visione standard; - lo scatto con iperfocale calcolata sul CdC del formato APS-C mostra una miglior nitidezza, tale che una stampa generata da questo file sarebbe –da una distanza di visione standard- praticamente indistinguibile da quella generata con lo scatto con m.a.f. su infinito. - lo scatto con iperfocale con CdC pari al CDm reale mostra un risultato praticamente identico a quello con m.a.f. su infinito: questo significa che tutte le informazioni aggiuntive eventualmente trasmesse dall’ottica focheggiando esattamente all’infinito non possono essere registrate dal nostro sensore. Un'immagine del genere può essere osservata da una distanza inferiore a quella standard. Da quest’ultima considerazione si deduce che –al fine di ottenere la massima qualità possibile con un soggetto tridimensionale- non è necessario eseguire una lunga serie scatti relativi a ciascun piano della scena (condizione teorica), ma è sufficiente eseguire un numero ridotto di scatti perché si sfrutta la profondità di campo ottenibile con un CdC pari al circolo di definizione massima (CDm reale). Utilizziamo il seguente caso pratico per mostrare i benefici derivanti da questa tecnica:
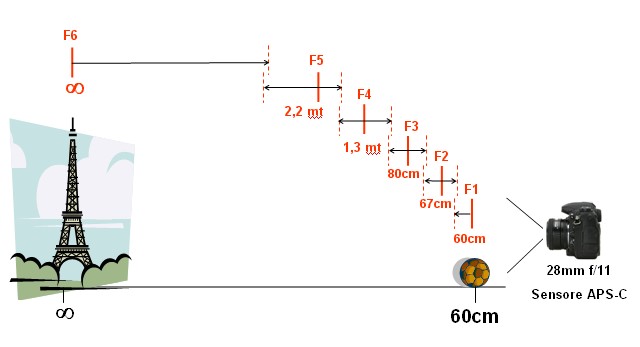
Si tratta di una classica situazione di ripresa: l’immagine è stata ripresa con un sensore APS-C e ottica di focale 28mm (42mm equiv.), cercando ottenere una profondità di campo sufficiente per coprire tutta la scena inquadrata, che si estende da circa 60cm all’infinito. Prendendo a riferimento il CdC del formato APS-C (0,0196mm), si sarebbe resa necessaria una chiusura del diaframma a f/32, con messa a fuoco impostata sull’iperfocale (1,25mt). Dato che f/32 è indisponibile, si è utilizzato il diaframma f/22 ammettendo il CdC del formato 35mm (0,0294mm), sempre con messa a fuoco sull’iperfocale (1,18mt). Nell’illustrazione seguente sono riportarti alcuni ritagli dell’immagine provenienti rispettivamente dalla zona di messa a fuoco, primo piano e sfondo:
Come risulta evidente, c’è una visibile perdita di qualità sui soggetti in primo piano e sullo sfondo rispetto al piano di messa a fuoco, che comunque non è ottimale considerando ciò che si può ottenere scattando a f/11. Per risolvere entrambi i problemi, si decide di effettuare una sequenza di sei scatti a f/11, con messa a fuoco così impostata:
La CdC utilizzata è quella del formato APS-C, che in pratica si ottiene scattando a f/11 e seguendo le tacche sul barilotto relative ad uno stop più aperto, ovvero f/8. La scelta di un CdC pari al CDm reale avrebbe richiesto un numero troppo elevato di scatti, per cui si è preferita una soluzione di buon compromesso tra qualità e rapidità di esecuzione. Tornando al nostro esempio, la scelta dello schema a sei scatti comporta molti vantaggi: - si passa da uno a ben 6 piani di messa a fuoco con “nitidezza reale” - si posiziona un piano di nitidezza sul primo piano ed uno sullo sfondo, zone nelle quali spesso si valuta con maggior attenzione la definizione dell’immagine - si utilizza un diaframma ottimale (f/11), che evita il problema della diffrazione - si adotta un CdC sufficiente per il formato utilizzato. Una volta realizzati gli scatti necessari, vediamo come ottenere in post-produzione l’immagine definitiva, con l’aiuto di PTGui.
La prima cosa che notiamo aprendo le immagini su livelli distinti di Photoshop è che, pur essendo state scattate su cavalletto, le immagini con messa a fuoco diversa non coincidono:
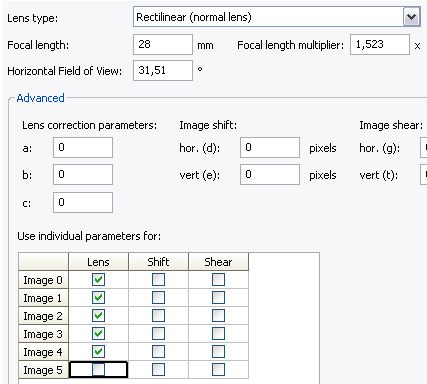
Da un'analisi più approfondita, è facile notare come i sei scatti siano caratterizzati da rapporti di ingrandimento leggermente diversi, fenomeno fisico dovuto alla diversa messa a fuoco. Serve dunque un software che esegua in maniera corretta il ridimensionamento degli scatti per renderli sovrapponibili. PTGui è in grado di svolgere perfettamente questo compito. Vediamo come. Si apre un nuovo progetto PTGui, quindi si inseriscono le 6 immagini che compongono il Focus stitch: nel nostro caso l’immagine “0” è quella con m.a.f. ravvicinata (60cm) mentre l’immagine “5” è quella con m.a.f. su infinito. PTgui dispone della funzione di rilevamento automatico dell’ottica utilizzata (dati EXIF), ma è sempre consigliabile controllare la loro correttezza. Nel pannello “Lens” si informa PTGui che le immagini 0-4 vanno trattate come “individual lens” (ottica individuale), ovvero potranno essere ottimizzate con valori diversi di FoV,a,b,c rispetto all’immagine 5:
Nel pannello “Panorama Settings” impostiamo la proiezione “rettilineare”, ovvero la stessa generata dall’ottica utilizzata:
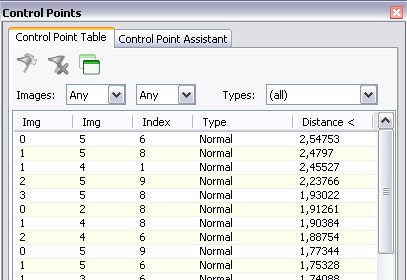
Si apre successivamente il pannello “Control Points”, e si avvia la generazione automatica dei punti di controllo dal menu “Control Points / Generate Control points for all images”. I punti di controllo vengono normalmente generati correttamente, ma si deve far attenzione che non siano stati presi riferimenti su soggetti che si sono mossi tra uno scatto e l’altro: in tal caso i punti incriminati devono essere rimossi.
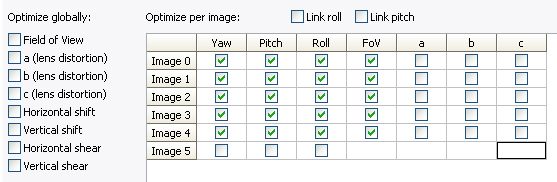
Nel pannello “Optimizer” (modalità avanzata) si impostano i seguenti parametri:
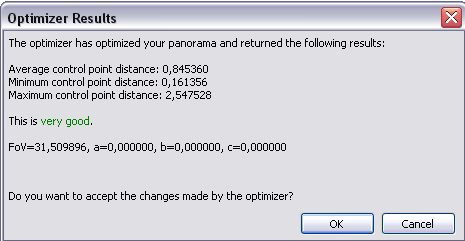
Come si vede, nessun parametro viene ottimizzato globalmente. A questo punto si lancia l’ottimizzazione (Run Optimizer) e si valutano i risultati:
L’errore medio è molto basso ed anche l’errore massimo è molto contenuto, dunque si può accettare di buon grado il lavoro svolto dall’Optimizer.
Successivamente, per controllare visivamente il lavoro svolto, si apre la finestra “Panorama editor” e si adatta il FoV complessivo al Fov dell’immagine, utilizzando il tasto “Fit Panorama”:
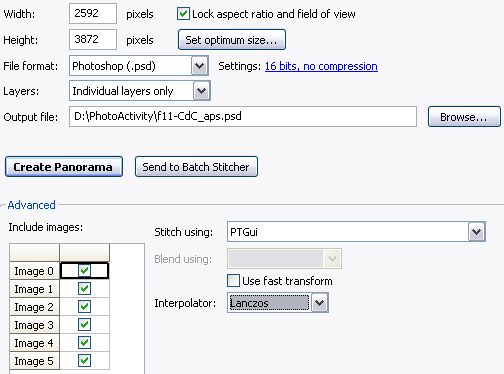
L’ultima fase è quella di creazione del file PSD finale:
Queste sono le scelte effettuate: - Height e Width sono impostate con le stesse dimensioni degli scatti originali Al termine dell'elaborazione la sovrapposizione tra gli scatti risulta perfetta, fatta ovviamente eccezione per gli elementi che si sono mossi tra uno scatto e il successivo:
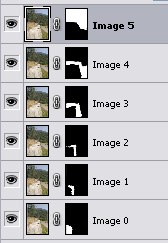
La fase di selezione delle aree più nitide di ciascun fotogramma si esegue con un software di photo-editing, capace di gestire i livelli e le maschere di livello: Photoshop è sicuramente il software di riferimento per questo tipo di applicazione. La tecnica è concettualmente semplice, ma quando il numero di livelli è elevato il tempo di lavorazione non è affatto trascurabile; l’esperienza insegna inoltre che molto dipende dal layout della scena inquadrata. In pratica si tratta lavorare con lo strumento "pennello" su ciascuna maschera di livello, in modo da nascondere (annerire) le aree sfocate o poco nitide, partendo dal livello più in alto. Ecco come si presenta la palette "livelli" dopo la lavorazione definitiva:
Come si vede, dell’immagine 5 (m.a.f. su infinito) è stato selezionato lo sfondo, mentre delle restanti immagini sono state selezionate porzioni che corrispondono a distanze sempre più ravvicinate.
Il guadagno ottenuto in termini nitidezza si commenta da solo. Per una miglior valutazione, è possibile scaricare l’immagine completa (formato jpeg qualità 10, dimensione del file 4 Mb). Viceversa, accettando un livello di nitidezza intermedio, si può optare per una serie di tre scatti con lo stesso CdC ma con diaframma f/22, dedicando due scatti al primo piano ed allo sfondo, più uno scatto intermedio. Questi sono i risultati:
Considerato il lavoro molto più ridotto sia in fase di ripresa che in fase di post-produzione, anche questa soluzione è da ritenersi molto vantaggiosa.
La gestione della nitidezza dei vari piani della scena, rimasta per decenni esclusivo appannaggio degli utilizzatori di attrezzature speciali (fotocamere a corpi mobili oppure ottiche Tilt/Shift), apre oggi le porte anche al “popolo” del piccolo formato grazie alla tecnica digitale del Focus Stitch. In questo articolo abbiamo mostrato il potenziale del Focus stitch, ma è importante conoscere anche i limiti pratici di questa tecnica, primo fra tutti la necessità di disporre di soggetti statici. In realtà questo limite è talvolta aggirabile, potendo contare su un po’ di esperienza in fase di ripresa ed in fase di post-produzione. Il concetto è che gli artefatti possono esistere, ma non devono essere individuabili anche dell’osservatore più smaliziato. Un altro limite si manifesta quando un soggetto vicino alla fotocamera si staglia direttamente su uno sfondo posto a distanza considerevolmente maggiore. In questi casi la soluzione perfetta non esiste, perché i margini sfocati del soggetto in primo piano (nello scatto con m.a.f. sullo sfondo) nascondono una porzione dello sfondo maggiore della superfice reale del soggetto stesso. Anche l’utilizzo delle menzionate attrezzature speciali non consente di rimediare il problema, perché regola di Scheimpflug in questi casi non trova applicazione.
|