| 28 Août 2005 |
Visiteur N 10346
| 28 Août 2005 |
Visiteur N 10346
Introduction:
Dans cet article nous comparons le rendu de 2 convertisseurs Raw: Camera Raw 3.0 et DCRaw 7.02. Camera Raw 3.0 est le convertisseur intégré à Adobe Photoshop CS2 et a été écrit par Thomas Knoll qui est l'un des auteurs de Photoshop. DCRaw par contre a été écrit par Dave Coffin, DCRaw par contre a été écrit par Dave Coffin, personnage peut-être moins connu. C'est un ingénieur en logiciel de Andover ( Massachusetts ) qui un jour, en février 1997, a décidé de décoder le format Raw de son appareil compact Canon PowerShot 600, pour obtenir de meilleurs résultats en ce qui concerne le JPEG généré par l'appareil. Il a ainsi décidé d'écrire son logiciel en ANSI C,qui est, dans l'absolu, l'un des langages de programmation les plus portés et évidemment compilable sur presque toutes les plateformes (Windows, Dos, Unix etc...). Depuis lors, il "s'est amusé" à décoder tous les formats Raw existants et a mis son code gratuitement à la disposition de tous. La liste des formats supportés est vraiment longue, comme vous pouvez le constater dans la page web dépouillée dédiée à DCRaw. La chose singulière est qu'il déclare ( et ça n'a pas été démenti, il n'y a donc pas de raison de ne pas le croire ) qu'une longue liste de décodeurs Raw utilise tout ou partie de son code. Parmi les noms les plus titrés, je rappellerai ACDSee, Cunulus par Canto, SilverFast, DCPro par Lasersoft Imaging, VueScan par Ed Hamrick et, écoutez bien, Adobe Photoshop, par conséquent Camera Raw objet de cet article. En général, en effet, quand un nouveau format Raw sort, DCRaw est d'abord mis à jour et tous les autres suivent. Comme je l'ai dit auparavant, il met son code source à disposition, pas le fichier exécutable, mais il y a cependant toujours quelqu'un qui le compile et le rend disponible pour tout le monde. Par conséquent, on trouve toujours quelquepart un dcraw.exe à lancer en ligne de commande sous Windows ou sous d'autres plateformes. Mais qu'a t'il de spécial ce programme? Voyons le ensemble.
Capteurs et interpolation
Les capteurs électroniques ne sont pas, de par leur nature, sensibles sélectivement dans le spectre, c'est à dire qu'afin qu'un pixel soit sensible au rouge, au vert ou au bleu, il faut interposer un filtre coloré sans lequel ne serait enregistrée que l'information de luminosité relative à tout le spectre, des 380 aux 720 nm (et même au-delà). Nous voyons ici l'exemple d'un capteur de chez Fuji avec un pixel de forme hexagonale.

Comme on le remarquera mieux dans la figure ci-dessous, les couleurs rouge, vert et bleu sont accolées et non pas superposées comme cela se produit dans les pellicules photographiques.

Comme vous l'aurez remarqué, il y a une prédominance de pixels verts, parce que l'oeil est plus critique aux détails de cette couleur. La figure ci-dessus montre la disposition classique de Bayer, c'est à dire avec un rapport de 2 pixels verts tous les 4 pixels. Il existe en réalité un capteur qui travaille d'une façon plus proche de la pellicule: celui de de chez Foveon. Il exploite la caractéristique du silicium qui est capable d'absorber la lumière de façon sélective, selon son épaisseur. En d'autres termes, le silicium lui même sert de filtre et les trois couleurs primaires sont disposées dans le sens vertical, comme démontré dans la figure ci-dessous.

Cette disposition simplifie la reconstruction de l'image, mais présente encore bien des difficultés de construction, en effet, il n'a encore été commercialisé aucun capteur d'une résolution supérieure à 3 MPixels (par couche) et de dimensions supérieures au format APS. La difficulté principale réside dans le fait de réussir à aligner parfaitement les pixels à la verticale. Cet inconvénient se traduit par une séparation insuffisante des couleurs, c'est à dire dans une saturation basse. Les techniques pour l'augmenter, cependant, augmentent aussi le bruit, pour lequel l'algorithme de reconstruction de l'image s'en trouve alourdi par le travail nécessaire pour réduire le "grain" électronique. La très grande majorité des capteurs du commerce se base sur la matrice de Bayer, typologie de capteur que nous traiterons dans cet article.
Dans la figure ci-dessous on peut noter ce que "voit" le capteur avec un filtre de Bayer (à gauche) et le résultat de l'image reconstruite (à droite).
 |
 |

En pratique, après avoir déclenché une photo, dans chaque cadre relatif aux trois couleurs Rouge Vert et Bleu, il manque des pixels qu'il faut interpoler. L'opération d'interpolation joue un rôle fondamental dans la définition de l'image finale. Le "Stanford Center for Image Systems Engineering" a publié une ètude sur les différentes méthodes d'interpolation. L'auteur de cette étude s'appelle Ting Chen et il l'a publiée durant l'hiver 1999. Voyons dans un bref résumé les résultats qui en ont émergé.
L'interpolation la plus simple possible est celle qui est montrée ci-dessous. Elle consiste simplement à "répliquer" les pixels voisins. En nous référant au tableau de la couleur verte, comme dans la figure, nous voyons comment à l'emplacement du pixel No 8 a été répété le pixel No 7 et ainsi de suite pour les autres pixels manquants. Il est évident qu'il ne faut pas nous attendre à une qualité d'image finale très élevée.
![]()
Voyons maintenant un type d'interpolation un peu plus intelligent. Ceci est le schéma de la matrice de Bayer. L'interpolation bilinéaire fonctionne comme ceci:

Nous supposons devoir produire un pixel vert à l'emplacement 8, où il y a le pixel B8. On peut s'en approcher avec la moyenne arithmétique des 4 pixels verts contigüs, c'est à dire:
G8 = (G3+G7+G9+G13) / 4
Aux emplacements des pixels verts, les pixels bleus et rouges ne peuvent être "moyennés arithmétiquement" qu'entre 2 pixels voisins, par exemple:
B7 = (B6+B8) / 2 ; R7 = (R2+R12) / 2
Tandis qu'aux autres emplacements ils peuvent être également "moyennés arithmétiquement" entre 4 pixels:
R8 = (R2+R4+R12+R14) / 4 ; B12 = (B6+B8+B16+B18) / 4
Avec ce schéma nous comprenons pourquoi quand nous photographions des objets avec des détails qui passent rapidement d'une couleur sombre à une couleur claire, apparaissent ces halos embêtants appelés "color fringing". C'est un défaut dû à l'interpolation, quand ce n'est pas la faute des aberrations chromatiques de l'objectif. En effet, il y a des lignes et des colonnes dans lesquelles aucun pixel rouge ou bleu n'est présent, desquelles naît un déphasage des lignes de continuité. Le capteur Foveon par contre est exempt de ce défaut. Fuji, pour limiter ce problème, a pensé à faire tourner les images de 45°. En effet, à cause de la gravité terrestre, il y a naturellement une prédominance de lignes verticales et horizontales plutôt qu'obliques. En enregistrant les images à 45° on évite des interpolations difficiles dans ces directions, cependant, dans la rotation nécessaire au redressement, on perd un peu d'informations. Ci-dessous un exemple de comment naît le "color fringing":

Il y a beaucoup d'autres méthodes d'interpolation possibles prises en considération dans l'étude de Ting Chen. Mais passons directement à celle qui s'est ensuite révélée la meilleure et bien évidemment plus compliquée que celles que l'on vient de voir: la méthode des gradiants à nombre variable.
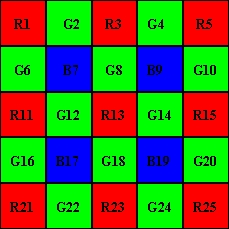
Nous supposons devoir extraire les valeurs du pixel vert et du pixel bleu à l'emplacement 13, c'est à dire G13 et B13. On définit 8 gradiants dans les directions cardinales suivantes:
Gradiant N = |G8 - G18| + |R3 - R13| + |B7 - B17| / 2 + |B9 - B19| / 2 + |G2 - G12| / 2 + |G4 - G14| / 2 ;
Gradiant E = |G14 - G12| + |R15 - R13| + |B9 - B7| / 2 + |B19 - B17| / 2 + |G10 - G8| / 2 + |G20 - G18| / 2;
Gradiant S = |G18 - G8| + |R23 - R13| + |B19 - B9| / 2 + |B17 - B7| / 2 + |G24 - G14| / 2 + |G22 - G12| / 2;
Gradiant W = |G12 - G14| + |R11 - R13| + |B17 - B19| / 2 + |B7 - B9| / 2 + |G16 - G18| / 2 + |G6 - G8| / 2;
Gradiant NE = |B9 - B17| + |R5 - R13| + |G8 - G12| / 2 + |G14 - G18| / 2 + |G4 - G8| / 2 + |G10 - G14| / 2;
Gradiant SE = |B19 - B7| + |B25 - R13| + |G14 - G8| / 2 + |G18 - G12| / 2 + |G20 - G14| / 2 + |G24 - G18| / 2;
Gradiant NW = |B7 - B19| + |R1 - R13| + |G12 - G18| / 2 + |G8 - G14| / 2 + |G6 - G12| / 2 + |G2 - G8| / 2;
Gradiant SW = |B17 - B9| + |R21 - R13| + |G18 - G14| / 2 + |G12 - G8| / 2 + |G22 - G18| / 2 + |G16 - G12| / 2;
Chacune de ces valeurs est un indice de combien est brusque le passage de la luminosité dans les directions indiquées par le nom, par rapport à l'emplacement 13. Plus la valeur est haute et plus le passage de la luminosité est sec.. Les directions avec une valeur plus haute sont à écarter, parce qu'elles introduiraient une grosse erreur si on les utilisait pour faire une moyenne, tandis que celles ayant une valeur plus basse sont plus dignes de foi si vous les utilisez pour faire la moyenne des valeurs manquantes (dans ce cas, du vert et du bleu). Faisons un exemple numérique, supposons que nous ayons trouvé ces valeurs:
|
Gradiant
|
N
|
E
|
S
|
W
|
NE
|
SE
|
NW
|
SW
|
|
Valeur
|
12
|
13
|
7
|
8
|
4
|
7
|
12
|
14
|
Bien. Maintenant on détermine un seuil: on fixe une valeur et tous les gradiants ayant une valeur plus haute seront écartés. Un tel seuil, que j'appelle S, vaut:
S = k1*Min + k2 * (Max - Min)
où k1 et k2 sont constants et dont les valeurs empiriques sont respectivement de 1.5 et 0.5
Min et Max sont les valeurs minima et maxima des gradiants, elles valent par conséquent 4 et 14 dans notre exemple.
S s'avère donc égal à 11 et le sous-ensemble de gradiants que je n'ai pas écarté sera:
Gradient subset = {S, W, NE, SE}
Ne considérons maintenant que les directions des gradiants déterminés, et définissons les valeurs moyennes dans de telles directions de la façon suivante:
|
G
|
B
|
R
|
|
|
S
|
G18
|
( B17 + B19 ) / 2
|
( R13 + R23 ) / 2
|
|
W
|
G12
|
( B7 + B17 ) / 2
|
( R11 + R13 ) / 2
|
|
NE
|
( G4 + G8 + G10 + G14 ) / 4
|
B9
|
( R13 + R5 ) / 2
|
|
SE
|
( G14 + G18 + G20 + G24 ) / 4
|
B19
|
( R13 + R25 ) / 2
|
Je définis et je calcule les sommes Gsum, Bsum et Rsum dans les 3 cas, que l'on obtient en faisant la somme des valeurs en colonnes du tableau ci-dessus, c'est à dire que dans notre exemple on obtient:
Gsum = G18 + G12 + ( G4 + G8 + G10 + G14 ) / 4 + ( G14 + G18 + G20 G24 ) / 4;
Bsum = ( B17 + B19 ) / 2 + ( B7 + B17 ) / 2 + B9 + B19;
Rsum = ( R13 + R23 ) / 2 + (R11 + R13 ) / 2 + ( R13 + R5 ) / 2 + ( R13 + R25 ) / 2;
Et finalement, je produis les valeurs recherchées:
G13 = R13 + ( Gsum - Rsum ) / 4;
B13 = R13 + ( Bsum - Rsum ) / 4;
où 4 est le nombre de gradiants considérés.
Observation: pour calculer la valeur du pixel vert, j'ai également utilisé la valeur lue du pixel rouge. Ceci parce que les 3 valeurs RGB, dans la réalité, s'avèrent très corrélationnelles. Ce concept est mieux expliqué dans le prochain article ( la même observation est valable pour les pixels bleus et les rouges ).
Pour produire les valeurs des pixels rouges et bleus aux emplacements des verts, on fait le même raisonnement, seules les définitions des gradiants initiaux changent, c'est à dire:

Gradiente N = |G3 - G13| + |B8 - B18| + |G7 - G17| / 2 + |G9 - G19| / 2 + |R2 - R12| / 2 + |R4 - R14| / 2 ;
Gradiente E = |R14 - R12| + |G15 - G13| + |G9 - G7| / 2 + |G19 - G17| / 2 + |B10 - B8| / 2 + |B20 - B18| / 2;
Gradiente S = |B18 - B8| + |G23 - G13| + |G19 - G9| / 2 + |G17 - G7| / 2 + |R24 - R14| / 2 + |R22 - R12| / 2;
Gradiente W = |R12 - R14| + |G11 - G13| + |G17 - G19| / 2 + |G7 - G9| / 2 + |B16 - B18| / 2 + |B6 - B8| / 2;
Gradiente NE = |G9 - G17| + |G5 - G13| + |R4 - R12| + |B10 - B18|;
Gradiente SE = |G19 - G7| + |G25 - G13| + |B20 - B8| + |R24 - R12|;
Gradiente NW = |G7 - G19| + |G1 - G13| + |B6 - B18| + |R2 - R14|;
Gradiente SW = |G17 - G9| + |G21 - G13| +|R22 - R14| + |B16 - B8|;
En somme, c'est décidément beaucoup plus compliqué. Mais cela en vaut-il la peine? Voyons. Pour avoir une estimation de l'erreur moyenne que l'on obtient avec les algorithmes différents, il a été utilisé une image échantillon et l'erreur quadratique moyenne évaluée est définie de cette façon:
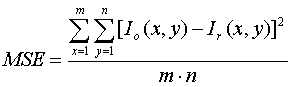
où m x n est la dimension de l'image, lo(x,y) représente la valeur réelle du pixel aux coordonnées x,y et lr(x,y) la valeur interpolée. Le tout normalisé à la valeur minimum trouvée qui est vraiment celle qui est relative à la méthode des gradiants et qui donc, s'avère être la meilleure (normalisé signifie "divisé par").
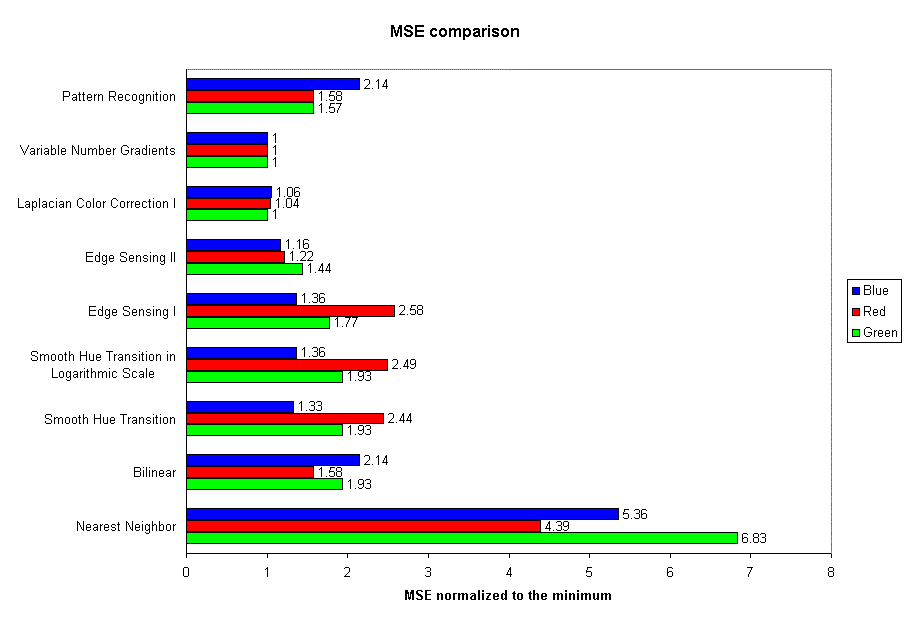
Voyons maintenant le coût informatique de notre candidat pour être le meilleur algorithme (en s'en remettant à 2 images échantillons):
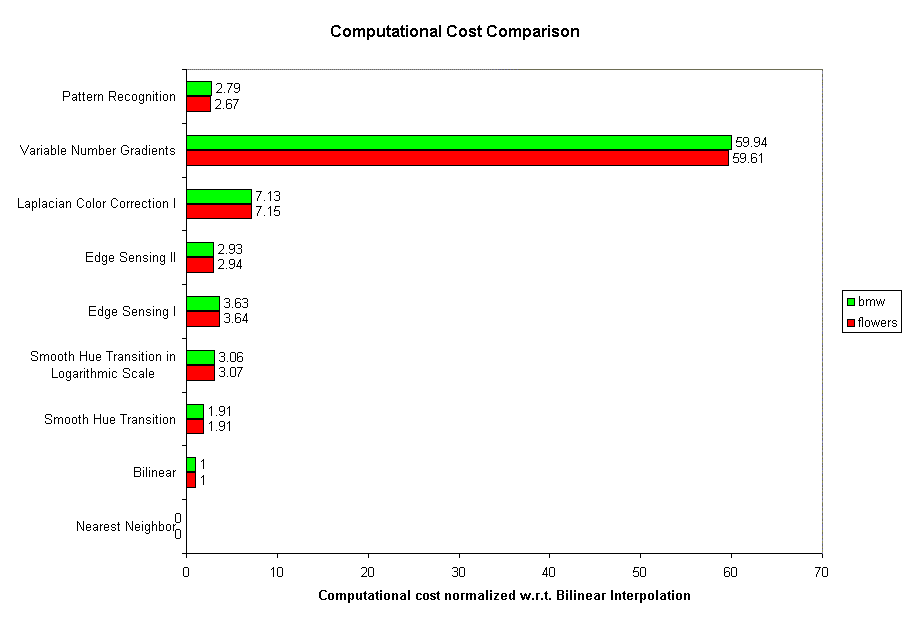
En informatique on parle de "coût d'un algorithme" pour indiquer le nombre d'opérations élémentaires nécessaires pour le mener à terme. Dans le graphique ci-dessus, il est tout normalisé au coût de l'algorithme bilinéaire (celui de duplication des pixels voisins n'a même pas été pris en considération pour sa qualité de bas niveau, et il lui a été attribué la valeur 0). Bien, notre candidat coûte vraiment beaucoup: l'ordinateur mettra environ 60 fois plus de temps que la méthode bilinéaire. Mais alors, cela en vaut-il vraiment la peine?
Comme vous l'aurez peut-être déjà deviné, DCRaw utilise cet algorithme, CameraRaw non. Je ne sais pas ce qu'utilise CameraRaw, mais ce n'est sûrement pas la méthode des gradiants. Je peux vraiment affirmer cela grâce à ce dernier graphique, en effet pour convertir une image de 6 Mpix avec DCRaw, mon Athlon 3200= met à peu près 5 secondes, avec CameraRaw environ 3.
Et maintenant, pour terminer voyons quelques exemples. Ces images ont été converties avec Unsharp Mask à zéro (avec CameraRaw, parce qu'avec DCRaw il n'est même pas possible d'appliquer ce filtre) et ensuite avec Photoshop j'ai appliqué le filtre de Smart Sharpen avec un rayon à 0.8, quantité à 150, Remove --> Lens Blur, More Accurate.
 |
 |
 |
 |
 |
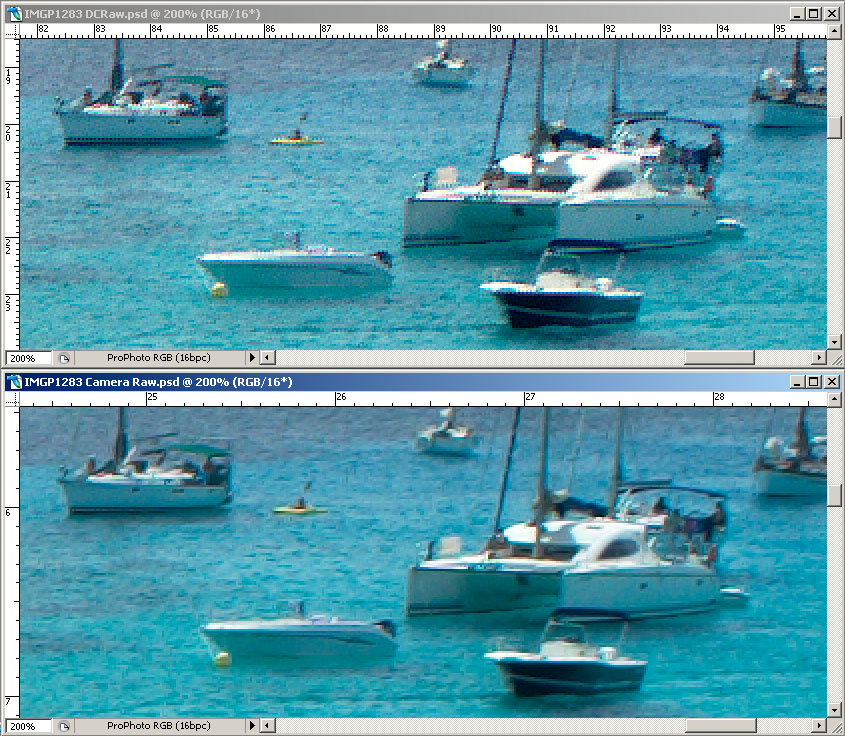 |
Hé bien je dirais que ça en vaut la peine.
Gestion de la couleur
Une des raisons pour laquelle DCRaw n'a pas eu le succès qu'il mérite est sûrement à cause du fait qu'il ne gère pas bien la couleur. D'abord, dans la conversion à 8 bits, il utilise un format pas vraiment courant qui est le PPM. Photoshop ne peut l'ouvrir que depuis la version CS2. Et puis il ne permet pas beaucoup de réglages comme les convertisseurs courants. Il a cependant une option qui permet de convertir à 16 bits au format PSD et en mode linéaire. Mais faisons un pas en arrière. Nous avons vu comment on gère la couleur pour un moniteur et une imprimante, mais au début, c'est à dire à partir du déclenchement et ensuite, que faut-il faire pour avoir des couleurs fidèles? La méthode la plus utilisée est probablement celle qui consiste à faire la balance des blancs manuellement, en pointant vers un petit carton neutre et peut-être en déclenchant/enregistrant en JPEG. Sincèrement, je n'avais jamais utilisé cette méthode parce que je ne m'attendais pas à des résultats exaltants, mais à la fin j'ai dû fair au moins 1 essai ne serait-ce que pour écrire cet article. J'ai photographié l'habituelle testchart à 24 cases, à la lumière et à l'ombre, en faisant la balance des blancs sur la troisième case grise en bas à partir de la gauche. L'appareil photo utilisé est un Pentax ist DS. Bien, pour quelques couleurs, on s'est approchés de la vérité (d'habitude les couleurs correctes sont dans la partie gauche de la testchart, elles ont été mesurées avec un spectrophotomètre et reconstruites avec Photoshop en utilisant les coordonnées Lab). Il doit bien y avoir des appareils qui vont mieux (ou qui vont moins bien) mais de toutes façons, ce n'est pas la bonne méthode pour obtenir des couleurs fidèles aux couleurs réelles.
JPEG

J'ai alors déclenché en Raw. Tout d'abord, avec CameraRaw, j'ai essayé d'amener les valeurs des 3 cases indiquées par les flêches, aux valeurs correctes obtenues en convertissant les valeurs Lab au profil Prophoto, qui est l'espace dans lequel je veux ouvrir mon "raw". Pour atteindre de telles valeurs, j'ai simplement déplacé le curseur de la page écran ci-dessous, je n'ai pas touché aux commandes "Calibrate", et dans "Curve" j'ai réglé une courbe linéaire égale à la bissectrice, c'est à dire qui ne fait rien.
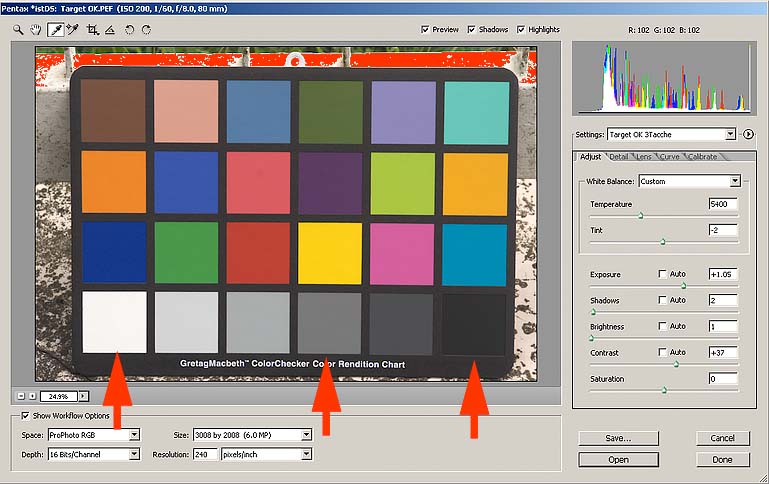
Voici les résultats
Camera Raw 3 Patches

La situation s'est un peu améliorée: au moins, les 3 cases que j'ai réglées sont bonnes. Et également d'autres cases ça et là. Mais pourquoi ne sont elles pas toutes bonnes? Essayons de le comprendre. Si j'éclaircis la testchart à 24 cases avec la luminance D50, les 24 coordonnées Lab des patches s'avèrent identifiées de façon univoque (si je change la luminance bien évidemment les coordonnées changeront également). Dans le profil sRGB, ces coordonnées Lab correspondent à des coordonnées RGB bien définies: la case rouge par exemple correspond à (179,49,75), la verte à (70,148,70) et ainsi de suite.
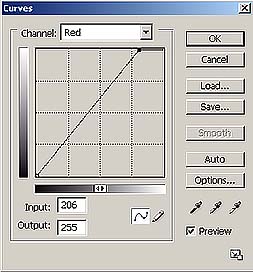
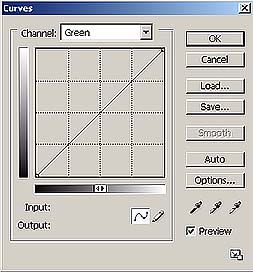
Si nous photographions la testchart dans ces conditions de luminance (c'est à dire avec une luminance qui approche le D50, c'est à dire le soleil par exemple), en déclenchant en Jpg à 8 bits, en réglant le profil sRGB et la balance pour lumière diurne, l'appareil devra changer les valeurs RGB lues dans les valeurs justes de l'espace sRGB. Il faut d'abord faire la balance des blancs, en utilisant les 6 cases grises de la testchart. Ceci équivaut à appliquer trois courbes semblables à celles ci-dessous, aux valeurs lues par l'appareil photo.
 |
 |
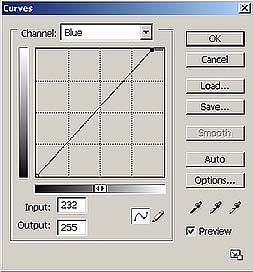 |
Le résultat est que les gris ont été rendus correctement, cependant les couleurs ne s'avèreront pas encore codées de façon juste, c'est à dire que les valeurs RGB des couleurs des autres cases ne seront pas encore relatives au profil sRGB. ,Il faut donc maintenant construire une fonction par points qui amène les valeurs lues aux valeurs correctes. Cette fonction peut être écrite sous forme tabellaire, réellement comme un profil ICC, et est appliquée par l'appareil après avoir fait la balance des blancs.
Si nous changeons le type d'éclairage et que nous faisons la balance des blancs avec l'appareil photo, nous changeons en pratique les 3 courbes de la balance que nous venons de voir, mais nous appliquons le même profil obtenu dans une situation d'éclairage différent, pour lequel nous n'obtiendrons pas une fidélité absolue des couleurs, surtout si le profil n'est pas très soigné, étant calculé en "runtime" par le processeur de l'appareil photo, qui s'en approche un peu pour accélérer le temps d'élaboration. Mémoriser dans l'appareil photo les différents réglages de balance des blancs standard, (Soleil, Nuages, Flash, Tungstène etc..) signifie ne mémoriser que les points du gris, relatifs à ces éclairages ( par conséquent que 3 nombres avec lesquels obtenir les courbes, c'est à dire, dans l'exemple ci-dessus, 206,255,232), ne signifie pas ré-écrire les profils obtenus dans les différentes situations d'éclairage. C'est pour cela que les couleurs obtenues ne seront pas très soignées. Si par contre nous voulons avoir à disposition un autre profil pour nos photos, de type Adobe RGB, il doit changer entièrement le tableau qui le représente dans l'appareil, ou l'algorithme qui la reconstruit. C'est pour cette raison que le nombre de profils à disposition est limité à 2 ou 3. En général, les profils mémorisés ne sont pas des profils ICC, mais ne sont que de simples algorithmes de conversion, qui dans le concept fonctionnent de la même façon que la conversion entre profils ICC à matrice mais ne sont pas très soignés.
CameraRaw fonctionne de façon analogue, mais est beaucoup plus versatile. Même Camera Raw associe des profils à chaque appareil photographique, en lisant le modèle spécifié dans les méta-données du fichier Raw. Pour chaque appareil photo, Camera Raw mémorise 2 profils différents. Un créé pour la luminance D65 (6500°K) et un pour la luminance A (2856°K). Le profil effectivement utilisé est interpolé entre les 2 mémorisés, selon la température de couleur de la scène. Une telle information peut être le point du blanc lu par l'appareil, si nous laissons « As shot » dans les réglages de la balance des blancs, ou bien nous pouvons régler manuellement la température en intervenant sur les curseurs « Température » et « Tint », ou nous pouvons encore faire une balance des blancs manuelle en utilisant l'instrument compte-gouttes sur une zone neutre de la scène. Les 2 profils associés à l'appareil photo, donc, changent de modèle à modèle, mais même 2 exemplaires du même modèle pourraient être caractérisés par des profils légèrement différents, pour des raisons de tolérance de fabrication. Avec Camera Raw il est possible de les calibrer de façon fine avec les contrôles de la page « Calibrate ».
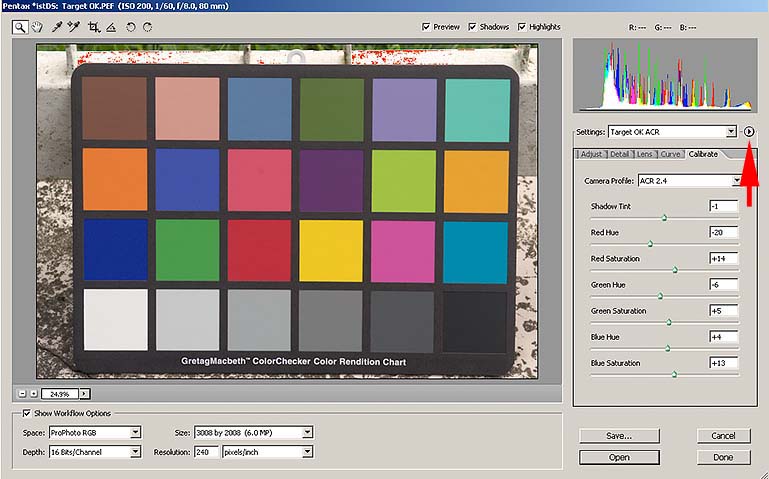
Et il y a même plus: si dans le petit bouton indiqué par la flèche nous réglons sur « Save New Camera Raw », Camera Raw se souviendra de ces corrections pour cet appareil photo en particulier, en l'identifiant univoquement avec le No de série qu'il lit toujours dans les méta-données des fichiers raw. Mais comment fait-on pour régler correctement les paramètres de ces profils? On peut le faire à la main, en essayant et ré-essayant jusqu'à ce que les valeurs RGB des 24 cases ne s'approchent pas le plus possible des valeurs réelles ou on peut utiliser un script java qui le fait pour nous. Il s'appelle ACR Calibrator, il est gratuit et fonctionne évidemment avec Photoshop. Il ne fait rien d'autre qu'ouvrir de nombreuses fois un fichier raw d'une photo de la testchart et, en variant à chaque fois un peu de paramètres, il trouve les valeurs optimales avec lesquelles reproduire fidèlement les 24 couleurs. Quand il termine,il crée une image avec les valeurs trouvées, comme celle ci-dessous:

Dans mon cas, il a mis 43 minutes et 44 secondes, ce qui est toujours moins que le temps que j'aurais mis en le faisant à la main. Voyons les résultats:
Camera Raw + ACR Calibrator

C'est sûrement beaucoup mieux. Quand on regarde en particulier la dernière ligne avec les cases grises, on remarque que le contraste est quasi parfait. Même les autres couleurs sont moyennement améliorées. Par conséquent, la bonne façon de travailler avec Camera Raw est celle d'exécuter ce type de calibration ne serait-ce que pour les situations de (re)prises fréquentes (lumière naturelle, réglage de pose ..etc) et de corriger éventuellement les images en phase d'ouverture en utilisant simplement les commandes de la page « Adjust ». Dans le cas où une reproduction très fidèle des couleurs est nécessaire, il faut toujours suivre cette procédure dans le premier déclenchement de chaque session.
Et maintenant revenons à DCRaw. Si en ligne de commande windows nous faisons: dcraw.exe nous obtenons les options disponibles:
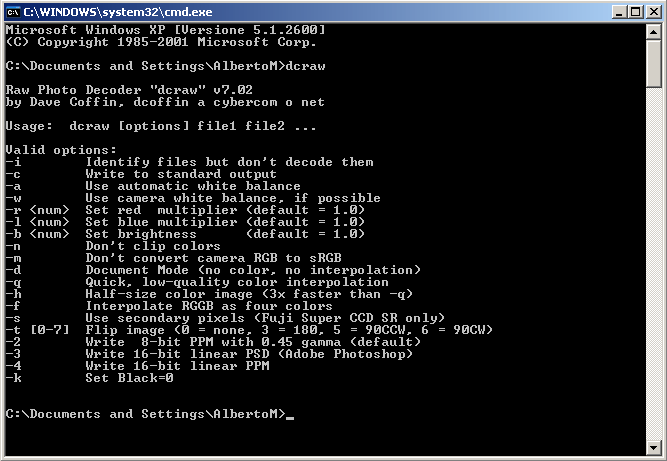
Si nous ne donnons explicitement aucune option, DCRaw convertit en format ppm en 8 bits et en sRGB (pas intégré). La conversion la plus intéressante cependant est celle en 16 bits au format de Photoshop PSD. Dans ce mode, les valeurs lues par l'appareil photo ne sont pas modifiées par des courbes bizarres, mais elles sont simplement transformées de 12 à 16 bits, c'est à dire que les valeurs lues dans l'appareil photo seront simplement multipliées par 216-12= 24 = 16 (pour l'instant, supposons que ce soit réellement comme ça, en réalité DCRaw fonctionne de façon un peu différente, comme c'est expliqué dans le prochain article). Une image convertie de cette façon a un gamma à peu près égal à 1, pour laquelle si nous lui assignions le profil sRGB, qui a un gamma de 2.2, nous la verrions sûrement sombre, comme dans l'exemple vu dans un article précédent. La solution est par conséquent de créer un profil ICC exprès pour notre appareil photo.
Cependant, il y a un problème. Quand on convertit au format PSD, DCRaw fait une opération qu'il ne devrait pas faire, c'est à dire qu'il fait une espèce de balance du point noir, qui dépend de l'image qu'il est en train de convertir. Cette opération est utile dans la conversion à 8 bits, parce qu'elle produit des couleurs neutres et contrastées, mais dans la conversion à 16 bits elles est simplement nuisible, dès l'instant où elle ne permet pas une conversion correcte des couleurs par l'intermédiaire des profils ICC. Je m'explique mieux avec un exemple graphique:
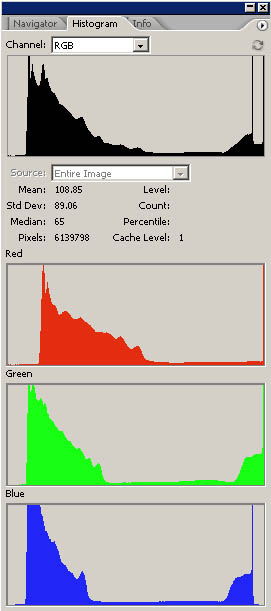 |
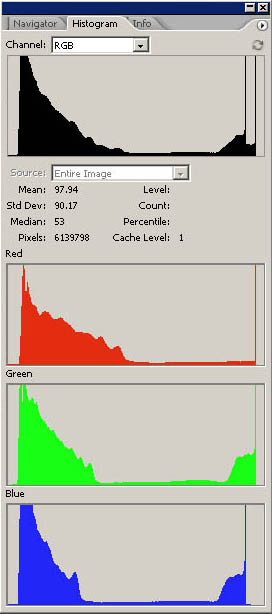 |
A gauche nous avons la conversion sans la balance du noir, à droite celle que fait DCRaw. Nous remarquons qu'il a pratiquement transféré les 3 niveaux RGB à gauche, de façon à générer un point du noir neutre, tandis que dans la conversion de gauche le noir s'avérait plus clair et sali par une dominante rouge. Cette opération serait aussi correcte, si ce n'est qu'elle n'est pas constante pour toutes les images, mais à chaque fois on calcule la valeur optimale à appliquer et elle transfère les niveaux de façon différente. De cette façon, un profil ICC créé pour un déclenchement particulier n'est pas applicable à d'autres déclenchements qui peuvent avoir des compensations du noir, différentes. J'ai résolu ce problème en allant modifier légèrement le code source de DCRaw qui, par chance, est disponible pour tout le monde. Si vous remarquez, entre les options disponibles de la ligne de commande,apparaît:
![]()
Cette option est une option que j'ai ajoutée, en effet vous ne la trouvez pas dans les versions exécutables de DCRaw qui parcourent le web. Elle sert simplement à éviter cette compensation automatique du noir.
Il faut également sélectionner l'option -m pour éviter la conversion en sRGB. Une telle conversion ne fonctionne que si nous convertissons en 8 bits, tandis qu'en 16 bits ce n'est qu'une opération inutile que DCRaw fait par défaut sans réaliser une vraie conversion en sRGB.
En définitive, pour convertir une série d'images raw, la commande est:
dcraw -m -k -3 *.pef
(pef est le format raw de Pentax)
J'ai ensuite créé le profil avec ProfilMaker en utilisant l'habituelle prise de la testchart.
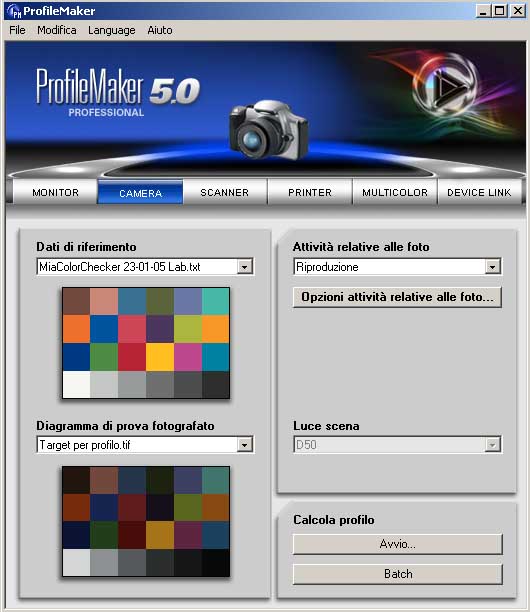
J'ai ensuite assigné le profil créé avec Photoshop et j'ai tout de suite converti en sRGB.
Voyons comment se présente la cible:
DCRaw + ProfileMaker

C'est sûrement la conversion la mieux réussie.
Si nous photographions dans des conditions d'éclairage très diverses, il faut créer un profil ad hoc. Dans ce cas par conséquent, la façon correcte de travailler est celle de créer des profils pour les situations de reprises plus fréquentes (lumière ambiante, flash etc...) et éventuellement de corriger les photos ainsi converties avec les instruments de Photoshop, en s'aidant peut-être avec l'insertion d'une testchart dans la scène. D'habitude, pour une reproduction plus soignée des couleurs, il faut se créer un profil pour chaque session de déclenchements.
Observation: en utilisant cette méthode, nous pouvons convertir notre image à un quelconque espace de travail, il suffit d'avoir le profil de destination. Avec Camera Raw, il y a quelques profils disponibles.
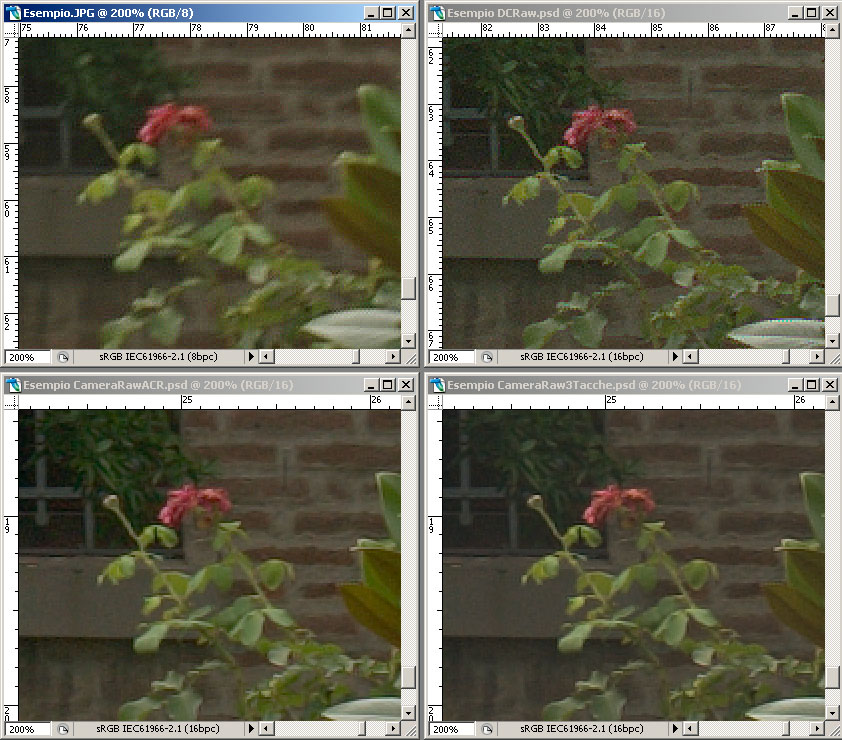
Voyons maintenant un déclenchement exécuté tout de suite après celui de la testchart, dans les 4 modes de conversion considérés:
JPEG

Camera Raw 3 Patches

Camera Raw + ACR Calibrator

DCRaw + ProfileMaker

Dans ce cas nous savons que les couleurs les plus fidèles sont celles du déclenchement « DCRaw + Profilemaker » parce que nous avons pu le constater directement sur la testchart. On peut remarquer, cependant, que cette conversion s'avère aussi être la moins contrastée. Dans la photo de tous les jours une reproduction très fidèle des couleurs peut apparaître peu brillante et contrastée, il est par conséquent facile de se retrouver à utiliser « curve » et « saturation » pour s'approcher au mieux de l'image à notre propre goût. C'est pour cela que ProfileMaker met à disposition des paramètres de contrôle en phase de création du profil, justement pour « corriger » contraste, saturation etc.. pour adapter le profil à un type particulier de prise de vue, en allant cependant au détriment de la fidélité des couleurs. C'est toujours pour cette raison que les appareils photo, quand ils déclenchent en JPEG, ne respectent pas trop fidèlement les couleurs, pour ne pas donner à l'utilisateur l'impression de contraste faible et de peu de vivacité des couleurs, on peut noter en effet que l'image JPEG est celle qui a les couleurs un peu plus vives.
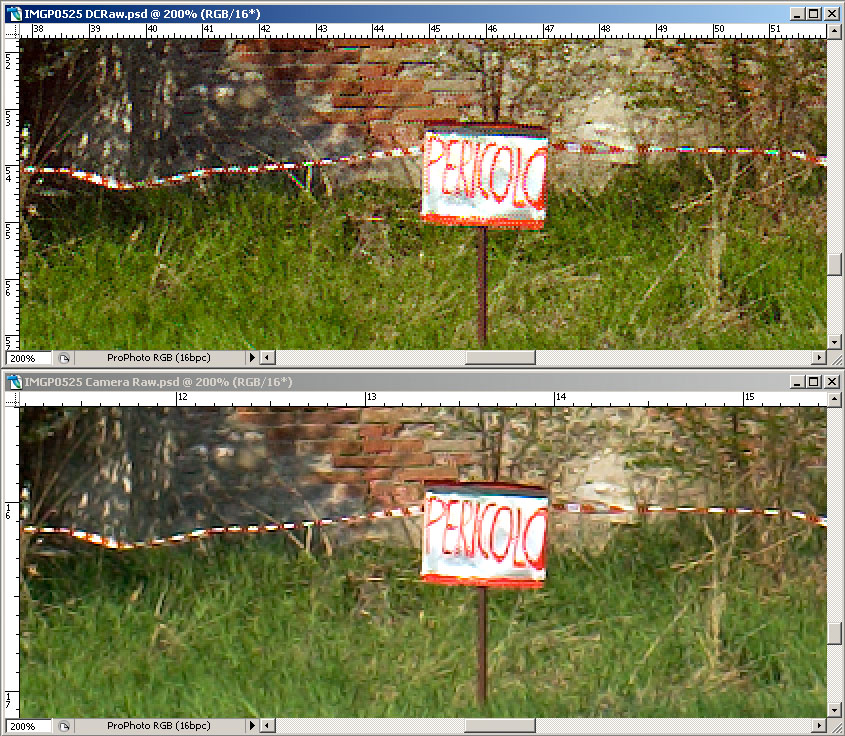
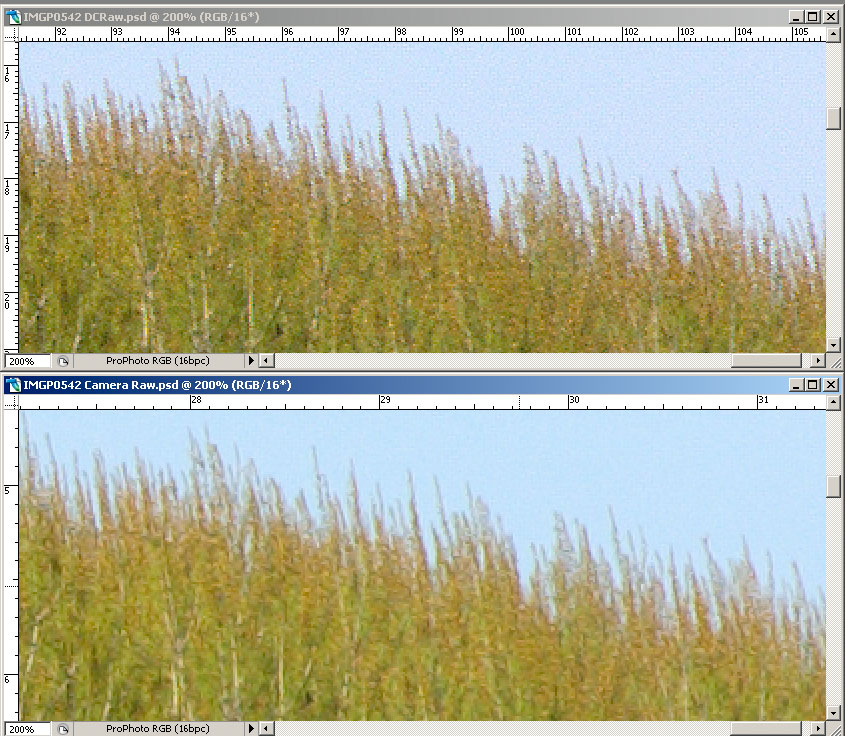
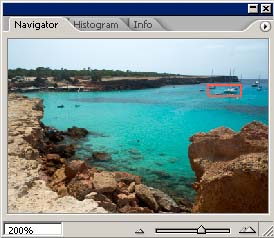
Voyons maintenant la même image agrandie à 200%. L'image JPEG a été prise en utilisant la valeur la plus basse de Unsharp Mask réglable sur l'appareil. Un filtre Smart Sharpen (quantité 250 et rayon 1) a ensuite été appliqué avec Photoshop CS2, tandis que pour les autres images, seules les valeurs de 150 et rayon 0.8 ont été utilisées
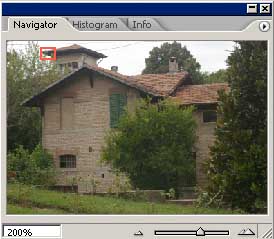 |
 |
 |
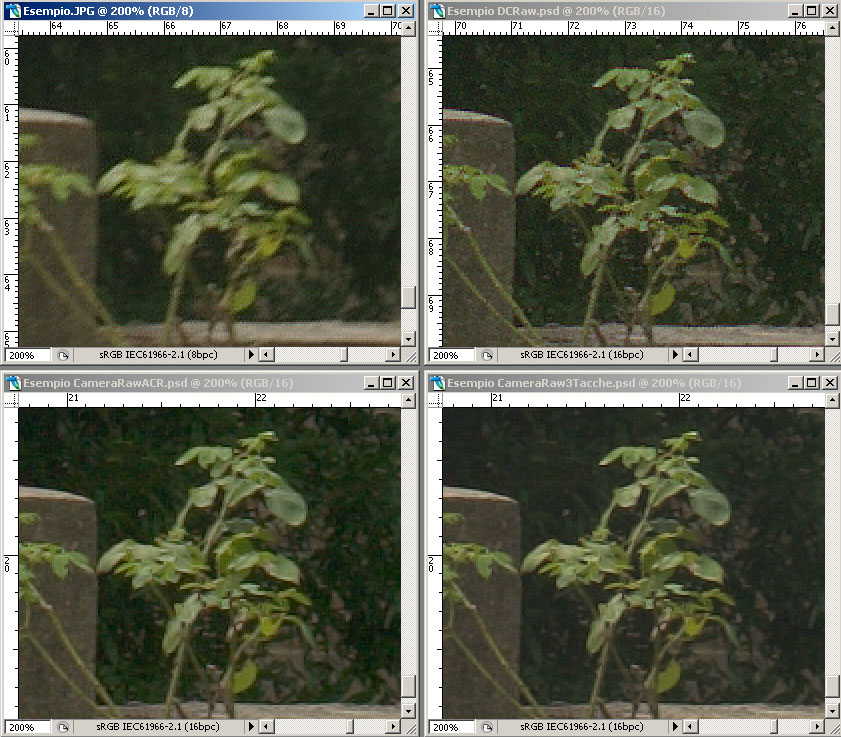 |
 |
 |
L'interpolation faite par l'appareil s'avère décidément de mauvaise qualité, on remarque en outre la compression JPEG, parce que la valeur de Smart Sharpen appliquée ensuite est élevée. Les couleurs relatives à l'image convertie avec DCRaw et à celles avec CameraRaw+ACR Calibrator s'avèrent très semblables, comme on pouvait s'y attendre.
CameraRaw applique par défaut une réduction du bruit et des phénomènes de color fringing que DCRaw ne fait pas: on peut le faire après coup avec les filtres appropriés.
A l'impression, une image convertie avec Camera Raw apparaît plus réaliste parce que les détails sont mieux définis, parce qu'en général moins d'artefacts (cristallisation) sont visibles et parce que ce grain électronique non corrigé la rend plus semblable à une photo chimique.
Observation: il est possible de créer un profil avec ProfileMaker même sur les images prises en JPEG ou converties avec Camera Raw, on a cependant, dans le premier cas, une perte de qualité par la compression à 8 bits au format JPEG, dans le second cas, c'est une opération de plus à faire: à ce stade il convient d'utiliser directement DCRaw qui fournit de meilleurs résultats dans le rendu des détails.
Autre observation: pour créer le profil de cet article, j'ai utilisé une testchart à 24 cases. Il en existe dans le commerce, des bien plus adaptées à ce but. Un exemple est la ColorChecker SG de GretagMacBeth qui a 140 cases et peut créer par conséquent des profils plus soignés.
Conclusion:
La reproduction de chaque partie de cet article est interdite sans la permission de l'auteur