| 28 Agosto 2005 |
Sei il visitatore numero 41876
| 28 Agosto 2005 |
Sei il visitatore numero 41876
Introduzione
In questo articolo confrontiamo la resa di due convertitori Raw: Camera Raw 3.0 e DCRaw 7.02. Camera Raw 3.0 è il convertitore integrato in Adobe Photoshop CS2 ed è stato scritto da Thomas Knoll, che è uno degli autori di Photoshop. DCRaw invece è stato scritto da Dave Coffin, personaggio forse meno conosciuto. E' un ingegnere del software di Andover (Massachusetts) che un giorno, nel Febbraio del 1997, ha deciso di decodificare il formato Raw della sua compatta Canon PowerShot 600, per avere risultati migliori rispetto al JPEG generato dalla macchina. Così ha deciso di scrivere il suo software in ANSI C, che è uno dei linguaggi di programmazione più portabili in assoluto, ovvero è compilabile praticamente su tutte le piattaforme (Windows, Dos, Unix, ecc). Da allora "si è divertito" a decodificare tutti i formati Raw esistenti e ha messo a disposizione di tutti, gratuitamente, il suo codice. L'elenco dei formati supportati è veramente lungo, come potete vedere nella scarna pagina web dedicata a DCRaw. La cosa singolare è che dichiara (e non è stato smentito quindi non c'è motivo di non credergli) che una lunga lista di decodificatori Raw utilizza il suo codice o parte del suo codice. Fra i nomi più blasonati ricordo ACDSee, Cunulus By Canto, SilverFast DCPro by LaserSoft Imaging ,VueScan by Ed Hamrick e, udite udite , Adobe Photoshop, quindi Camera Raw oggetto di questo articolo. In genere, infatti, quando esce un nuovo formato raw, prima viene aggiornato DCRaw, e a seguire tuti gli altri. Come ho detto prima mette a disposizione il codice sorgente, non il file eseguibile, però c'è sempre qualcuno che lo compila e lo rende disponibile a tutti. Quindi si trova sempre, da qualche parte, un dcraw.exe da lanciare dalla linea di comando di Windows o da altre piattaforme. Ma cos' ha di speciale questo programma? Vediamolo insieme.
Sensori e Interpolazione
I sensori elettronici , per loro natura, non sono sensibili selettivamente nello spettro, cioè, affinchè un pixel sia sensibile al rosso o al verde o al blu, è necessario interporre un filtro colorato, senza il quale verrebbe registrata la sola informazione di luminosità relativa a tutto lo spettro, dai 380 ai 720 nm (e anche oltre). Qui vediamo l'esempio di un sensore della Fuji con i pixel di forma esagonale.

Come si può notare meglio nella figura sotto, i colori rosso, verde e blu sono affiancati, e non sovrapposti come avviene nelle pellicole fotografiche.

Se notate c'è una predominanza di pixel verdi, in quanto l'occhio è più critico ai dettagli di questo colore. La figura sopra mostra la classica disposizione di Bayer, ovvero con il rapporto di due pixel verdi ogni quattro. In realtà esiste anche un sensore che lavora in modo più simile alla pellicola: quello della Foveon. Sfrutta la caratteristica del silicio di assorbire la luce in modo selettivo, a seconda del suo spessore. In altre parole il silicio stesso funge da filtro e i tre colori primari sono disposti in senso verticale, come mostrato nella figura sotto.

Questa disposizione semplifica la ricostruzione dell'immagine, ma presenta ancora molte difficoltà costruttive, infatti non è ancora stato messo in commercio un sensore con risoluzione maggiore di 3 MPixel (per ogni strato) e con dimensioni maggiori del formato APS. La difficoltà principale sta nel fatto di riuscire ad allineare perfettamente i pixel in verticale. Questo inconveniente si traduce in una scarsa separazione dei colori, ovvero in una bassa saturazione. Le tecniche per aumentarla, però, esaltano anche il rumore, per cui l'algoritmo di ricostruzione dell' immagine risulta appesantito dal lavoro necessario per ridurre la "grana" elettronica. La stragrande maggioranza dei sensori in commercio si basa sulla matrice di Bayer, tipologia di sensore che tratteremo in questo articolo.
Nella figura sotto si può notare cosa "vede" il sensore con filtro di Bayer (a sinistra), e come risulta l'immagine una volta ricostruita (a destra).
 |
 |
Sotto abbiamo lo schema dell'operazione di ricostruzione dell'immagine, che viene chiamata demosaicizzazione.

In pratica, dopo aver scattato una foto, in ogni quadro, relativo ai tre colori Red Green Blue, mancano dei pixel che bisogna interpolare. L'operazione di interpolazione gioca un ruolo fondamentale nella definizione dell'immagine finale. Lo "Stanford Center for Image Systems Engineering" ha pubblicato uno studio sui diversi metodi di interpolazione. L'autore di questo studio si chiama Ting Chen e lo ha pubblicato nell'inverno del 1999. Vediamo in un breve riassunto i risultati che sono emersi .
L'interpolazione più semplice possibile è quella mostrata sotto. Consiste semplicemente nel "replicare" i pixel vicini. Riferendoci al quadro del verde, come nella figura, vediamo come nella posizione del pixel numero 8 sia stato ripetuto il pixel numero 7 e così via anche per gli altri pixel mancanti. E' ovvio che non ci aspetteremo una qualità molto elevata nell'immagine finale.
![]()
Vediamo ora un tipo di interpolazione un po' più intelligente. Questo è lo schema della matrice di Bayer. L'interpolazione bilineare funziona così:

supponiamo di dover ricavare il pixel verde nella posizione 8, dove c'è il pixel blu B8. Lo possiamo approssimare con la media aritmetica dei 4 pixel verdi intorno, ovvero:
G8 = (G3+G7+G9+G13) / 4
Nelle posizioni dei pixel verdi, i pixel blu e rossi possono essere mediati solo fra due pixel vicini, per esempio:
B7 = (B6+B8) / 2 ; R7 = (R2+R12) / 2
Mentre nelle altre posizioni possono anch'essi essere mediati fra quattro pixel:
R8 = (R2+R4+R12+R14) / 4 ; B12 = (B6+B8+B16+B18) / 4
Da questo schema si capisce perchè quando fotografiamo oggetti con dettagli che passano rapidamente da un colore scuro a uno chiaro , escono quegli aloni fastidiosi chiamati "color fringing". E' un difetto dovuto all'interpolazione, quando la colpa non è delle aberrazioni cromatiche dell'obiettivo. Infatti ci sono righe e colonne in cui non è presente nessun pixel rosso o blu, da cui nasce uno sfasamento delle linee di discontinuità. Il sensore Foveon invece è privo di questo difetto. La Fuji, per limitare il problema, ha pensato di ruotare le immagini di 45 gradi. Infatti a causa della gravità terrestre, in natura c'è una predominanza di linee verticali e orizzontali piuttosto che oblique. Registrando le immagini a 45 gradi si evitano interpolazioni difficili lungo queste direzioni, però, nella rotazione necessaria al raddrizzamento, si perde un po' di informazione. Sotto un esempio di come nasce il color fringing :

Ci sono tanti altri metodi di interpolazione possibili presi in considerazione nello studio di Ting Chen. Ma passiamo direttamente a quello che poi è risultato il migliore, ed anche ovviamente più complicato di quelli appena visti: il metodo dei gradienti a numero variabile.
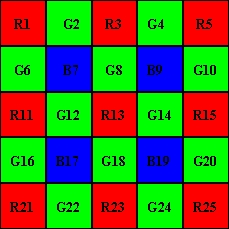
Supponiamo di dover ricavare i valori del pixel verde e di quello blu nella posizione 13, ovvero G13 e B13. Si definiscono 8 gradienti nelle direzioni cardinali seguenti:
Gradiente N = |G8 - G18| + |R3 - R13| + |B7 - B17| / 2 + |B9 - B19| / 2 + |G2 - G12| / 2 + |G4 - G14| / 2 ;
Gradiente E = |G14 - G12| + |R15 - R13| + |B9 - B7| / 2 + |B19 - B17| / 2 + |G10 - G8| / 2 + |G20 - G18| / 2;
Gradiente S = |G18 - G8| + |R23 - R13| + |B19 - B9| / 2 + |B17 - B7| / 2 + |G24 - G14| / 2 + |G22 - G12| / 2;
Gradiente W = |G12 - G14| + |R11 - R13| + |B17 - B19| / 2 + |B7 - B9| / 2 + |G16 - G18| / 2 + |G6 - G8| / 2;
Gradiente NE = |B9 - B17| + |R5 - R13| + |G8 - G12| / 2 + |G14 - G18| / 2 + |G4 - G8| / 2 + |G10 - G14| / 2;
Gradiente SE = |B19 - B7| + |B25 - R13| + |G14 - G8| / 2 + |G18 - G12| / 2 + |G20 - G14| / 2 + |G24 - G18| / 2;
Gradiente NW = |B7 - B19| + |R1 - R13| + |G12 - G18| / 2 + |G8 - G14| / 2 + |G6 - G12| / 2 + |G2 - G8| / 2;
Gradiente SW = |B17 - B9| + |R21 - R13| + |G18 - G14| / 2 + |G12 - G8| / 2 + |G22 - G18| / 2 + |G16 - G12| / 2;
Ciascuno di questi valori è un indice di quanto brusco sia il passaggio di luminosità nelle direzioni indicate dal nome, rispetto alla posizione 13. Più alto è il valore e più secco è il passaggio di luminosità. Le direzioni con valore più alto sono da scartare, perchè introdurrebbero un errore grande se le utilizzassimo per fare una media, mentre quelle con valore più basso sono più attendibili se utilizzate per mediare i valori mancanti (in questo caso del verde e del blu). Facciamo un esempio numerico, supponiamo di avere trovato questi valori:
|
Gradiente
|
N
|
E
|
S
|
W
|
NE
|
SE
|
NW
|
SW
|
|
Valore
|
12
|
13
|
7
|
8
|
4
|
7
|
12
|
14
|
Bene. Ora si determina una soglia: si fissa un valore e tutti i gradienti con valore più alto saranno scartati. Tale soglia, che chiamo S, vale:
S = k1*Min + k2 * (Max - Min)
dove k1 e k2 sono costanti il cui valore empirico è rispettivamente 1.5 e 0.5
Min e Max sono i valori minimo e massimo dei gradienti, quindi nel nostro esempio valgono 4 e 14.
S dunque risulta uguale a 11 e il sottoinsieme di gradienti che non ho scartato sarà:
Gradient subset = {S, W, NE, SE}
Ora considero solo le direzioni dei gradienti individuati, e definisco i valori medi in tali direzioni nel modo seguente:
|
G
|
B
|
R
|
|
|
S
|
G18
|
( B17 + B19 ) / 2
|
( R13 + R23 ) / 2
|
|
W
|
G12
|
( B7 + B17 ) / 2
|
( R11 + R13 ) / 2
|
|
NE
|
( G4 + G8 + G10 + G14 ) / 4
|
B9
|
( R13 + R5 ) / 2
|
|
SE
|
( G14 + G18 + G20 + G24 ) / 4
|
B19
|
( R13 + R25 ) / 2
|
Definisco e calcolo le somme Gsum, Bsum e Rsum nei tre casi, che si ottengono sommando i valori incolonnati nella tabella sopra, cioè nel nostro esempio si ottiene:
Gsum = G18 + G12 + ( G4 + G8 + G10 + G14 ) / 4 + ( G14 + G18 + G20 G24 ) / 4;
Bsum = ( B17 + B19 ) / 2 + ( B7 + B17 ) / 2 + B9 + B19;
Rsum = ( R13 + R23 ) / 2 + (R11 + R13 ) / 2 + ( R13 + R5 ) / 2 + ( R13 + R25 ) / 2;
E finalmente ricavo i valori cercati:
G13 = R13 + ( Gsum - Rsum ) / 4;
B13 = R13 + ( Bsum - Rsum ) / 4;
dove 4 è il numero di gradienti considerati.
Osservazione: per calcolare il valore del pixel verde ho utilizzato anche il valore letto del pixel rosso. Questo perchè i tre valori RGB, nella realtà, risultano molto correlati. Questo concetto è spiegato meglio nel prossimo articolo (la stessa osservazione vale per i pixel blu e rossi).
Per ricavare il valori dei pixel rossi e blu nelle posizioni dei verdi si fa lo stesso ragionamento, cambiano solo le definizioni dei gradienti iniziali, ovvero:

Gradiente N = |G3 - G13| + |B8 - B18| + |G7 - G17| / 2 + |G9 - G19| / 2 + |R2 - R12| / 2 + |R4 - R14| / 2 ;
Gradiente E = |R14 - R12| + |G15 - G13| + |G9 - G7| / 2 + |G19 - G17| / 2 + |B10 - B8| / 2 + |B20 - B18| / 2;
Gradiente S = |B18 - B8| + |G23 - G13| + |G19 - G9| / 2 + |G17 - G7| / 2 + |R24 - R14| / 2 + |R22 - R12| / 2;
Gradiente W = |R12 - R14| + |G11 - G13| + |G17 - G19| / 2 + |G7 - G9| / 2 + |B16 - B18| / 2 + |B6 - B8| / 2;
Gradiente NE = |G9 - G17| + |G5 - G13| + |R4 - R12| + |B10 - B18|;
Gradiente SE = |G19 - G7| + |G25 - G13| + |B20 - B8| + |R24 - R12|;
Gradiente NW = |G7 - G19| + |G1 - G13| + |B6 - B18| + |R2 - R14|;
Gradiente SW = |G17 - G9| + |G21 - G13| +|R22 - R14| + |B16 - B8|;
Insomma, è decisamente molto più complicato. Ma ne vale la pena? Vediamo. Per avere una stima dell'errore medio che si ottiene con i vari algoritmi è stata utilizzata un'immagine campione ed è stato valutato l'errore quadratico medio MSE così definito:
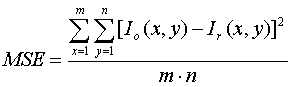
dove m x n è la dimensione dell'immagine, Io(x,y) rappresenta il valore vero dei pixel alle coordinate x,y e Ir(x,y) il valore interpolato. Il tutto normalizzato al valore minimo trovato che è proprio quello relativo al metodo dei gradienti e che dunque risulta il migliore (normalizzato significa "diviso per" ).
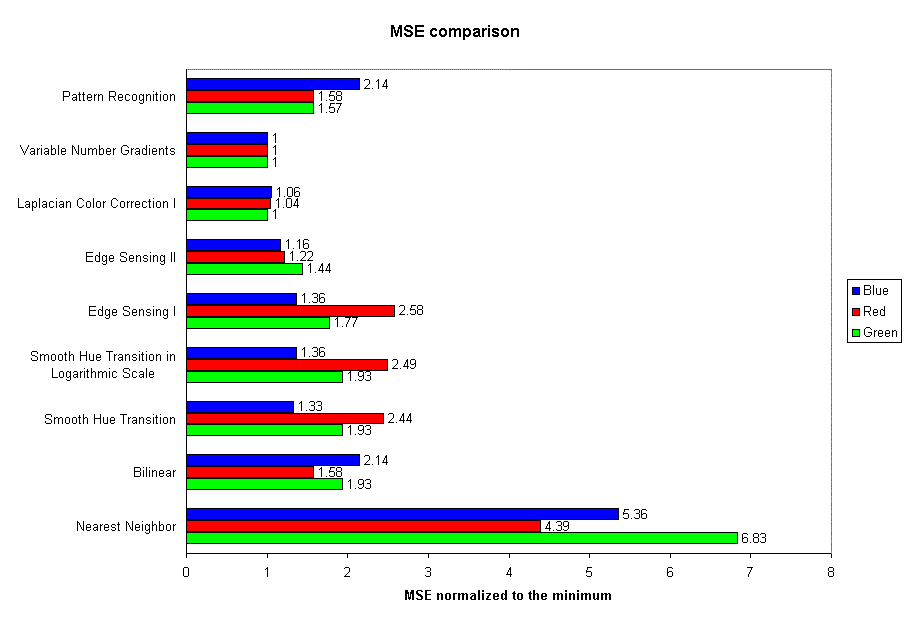
Vediamo ora il costo computazionale del nostro candidato ad essere il miglior algoritmo (riferito a due immagini campione):
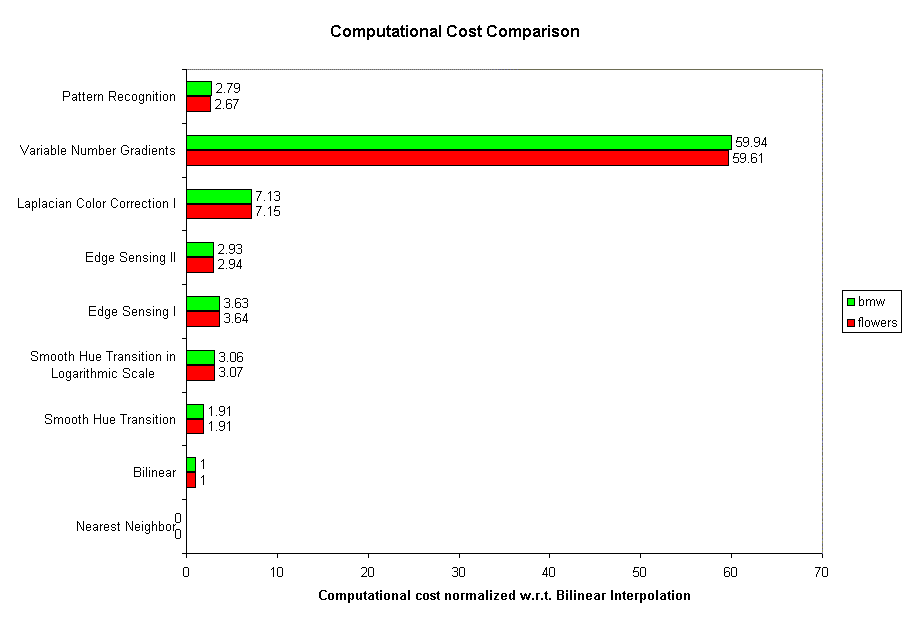
In informatica si parla di costo di un algoritmo per indicare il numero di operazioni elementari necessarie a portarlo a termine. Nel grafico sopra è tutto normalizzato al costo dell'algoritmo bilineare (quello di replicazione dei pixel vicini non è stato neanche preso in considerazione per la sua bassa qualità, e gli è stato assegnato il valore 0). Beh, il nostro candidato costa davvero tanto: il computer impiegherà un tempo circa 60 volte maggiore rispetto al metodo bilineare. Ma allora ne vale veramente la pena?
Come forse avrete già intuito DCRaw utilizza questo algoritmo, CameraRaw no. Non so cosa utilizzi CameraRaw, ma sicuramente non il metodo dei gradienti. Questo lo posso affermare proprio grazie a quest'ultimo grafico, infatti per convertire un'immagine da 6 Mpix con DCRaw il mio Athlon 3200+ impiega circa 5 secondi, con CameraRaw circa 3.
E ora, finalmente, vediamo qualche esempio. Queste immagini sono state convertite con Unsharp Mask a zero (in Camera Raw, perchè in DCRaw non è nemmeno possibile applicare questo filtro) e successivamente con Photoshop ho applicato il filtro di Smart Sharpen con raggio a 0.8, quantità a 150 , Remove --> Lens Blur , More Accurate.
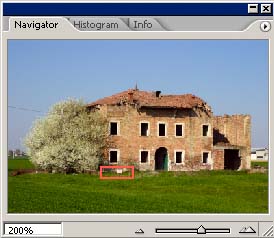 |
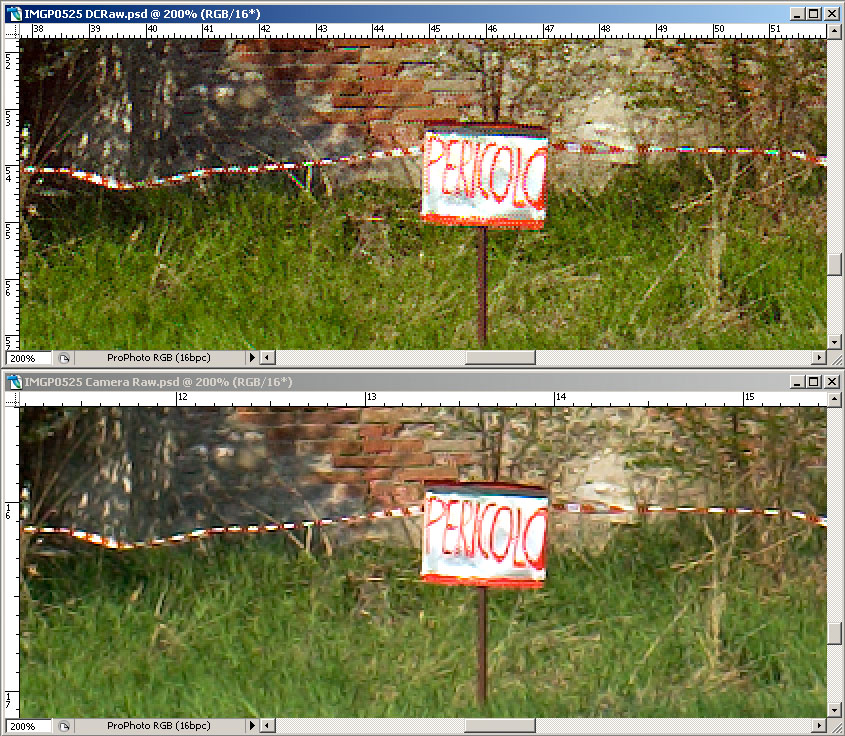 |
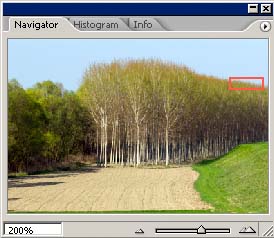 |
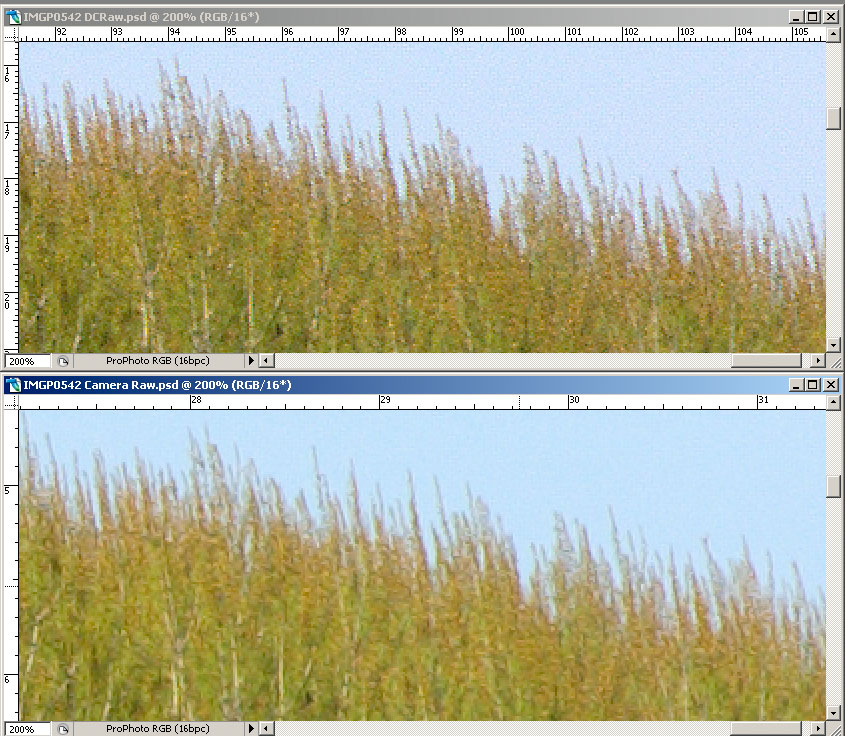 |
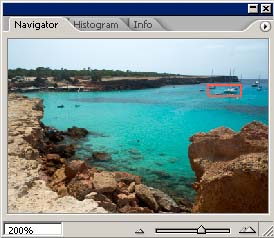 |
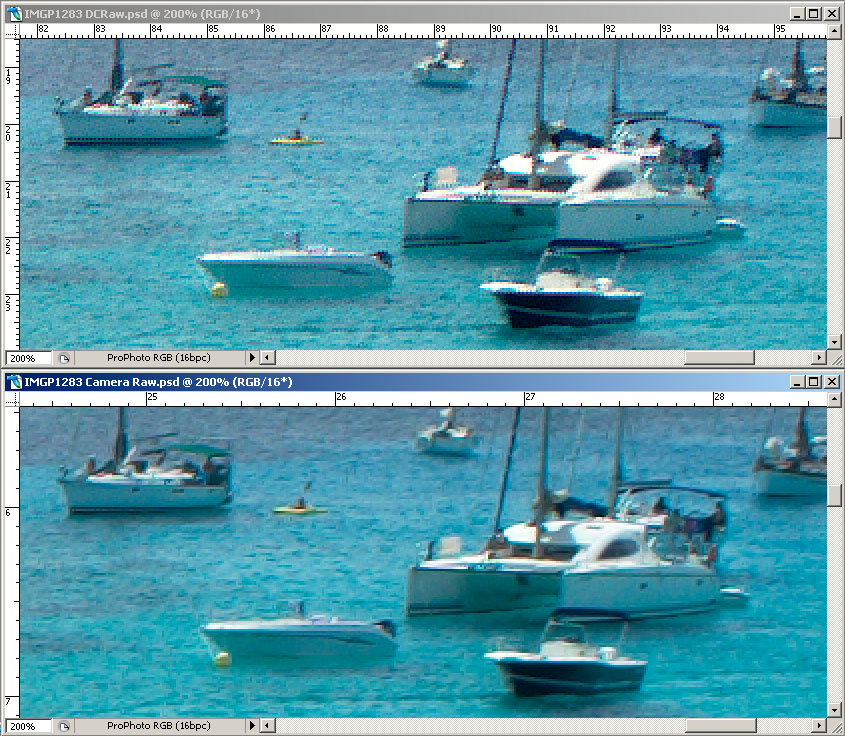 |
Beh, direi proprio che ne vale la pena.
Gestione del colore
Uno dei motivi per cui DCRaw non ha avuto il successo che si merita è sicuramente il fatto che non gestisce molto bene il colore. Innanzi tutto nella conversione a 8 bit utilizza un formato non proprio comune che è il PPM. Photoshop lo può aprire solo dalla versione CS2. E poi non consente tante regolazioni come i convertitori concorrenti. Però ha un'opzione che permette di convertire a 16 bit in formato PSD e in modo lineare. Ma facciamo un passo indietro. Abbiamo visto come si gestisce il colore per un monitor e per una stampante, ma all'inizio, cioè dal momento dello scatto in poi, cosa bisogna fare per avere colori fedeli? Probabilmente il metodo più utilizzato è quello di fare il bilanciamento del bianco manuale, puntando un cartoncino neutro e magari scattando in JPEG. Sinceramente questo metodo non lo avevo mai utilizzato, perchè non mi aspettavo risultati esaltanti, ma alla fine ho dovuto fare almeno una prova, se non altro per scrivere questo articolo. Ho fotografato la solita testchart a 24 tacche, all' aperto e all'ombra, facendo il bilanciamento del bianco sulla terza tacca grigia in basso a partire da sinistra. Ho scattato con varie esposizioni a intervalli di 1/3 di stop per essere sicuro di centrare quella giusta. La macchina utilizzata è una Pentax *ist DS. Beh, in qualche colore c'è anche andata vicina (i colori corretti al solito sono nella parte sinistra delle patches, sono stati misurati direttamente sulla testchart con uno spettrofotometro e ricostruiti in Photoshop utilizzando le coordinate Lab). Ci saranno sicuramente macchine che vanno meglio (e che vanno peggio), ma in ogni caso questo non è un buon metodo per ottenere colori fedeli a quelli reali.
JPEG

Allora ho scattato in raw. Per prima cosa, con Camera Raw, ho provato di portare i valori delle tre tacche indicate dalle frecce ai valori corretti, ottenuti convertendo i valori Lab al profilo Prophoto, che è lo spazio in cui voglio aprire il mio raw. Per raggiungere tali valori ho spostato solo i cursori della videata sotto, non ho toccato i comandi di "Calibrate", e in "Curve" ho impostato una curva lineare uguale alla bisettrice, cioè che non fa niente.
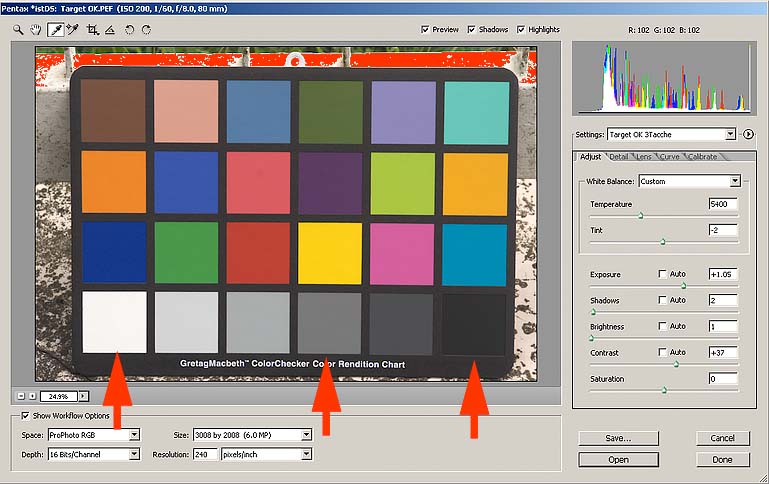
Questi i risultati:
Camera Raw 3 Patches

La situazione è un po' migliorata: almeno le tre tacche che ho regolato sono a posto. E anche qualche altra tacca qua e là. Ma perchè non sono venute bene tutte? Vediamo di capirlo.
Se illumino la testchart a 24 tacche con l'illuminante D50, le 24 coordinate Lab delle patches risultano identificate in modo univoco (se cambio illuminante ovviamente le coordinate cambieranno). Nel profilo sRGB, queste coordinate Lab corrispondono a coordinate RGB ben definite: per esempio la tacca rossa corrisponde a (179,49,75), quella verde a (70,148,70) e così via.
Se fotografiamo la testchart in quelle condizioni di illuminazione (cioè con un illuminante che approssimi il D50, quindi per esempio al sole), scattando in JPEG a 8 bit, impostando il profilo sRGB e il bilanciamento per luce diurna, la macchina dovrà cambiare i valori RGB letti nei valori giusti nello spazio sRGB.
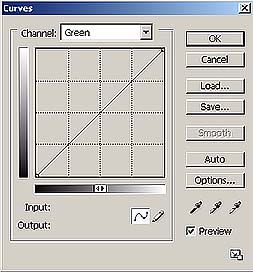
Per prima cosa occorre fare il bilanciamento del bianco, utilizzando le 6 tacche grigie della testchart. Questo equivale ad applicare tre curve simili a quelle sotto, ai valori letti dalla fotocamera.
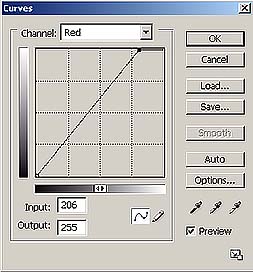 |
 |
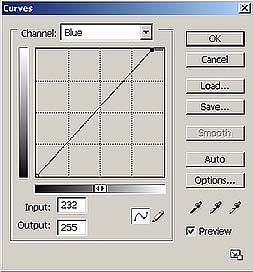 |
Il risultato è quello di aver reso i grigi correttamente, però i colori non risulteranno ancora codificati nel modo giusto, cioè i valori RGB dei colori delle altre tacche non saranno ancora quelli relativi al profilo sRGB. Quindi occorre ora costruire una funzione per punti che porti i valori letti nei valori corretti. Questa funzione può essere scritta in forma tabellare, proprio come un profilo ICC, e viene applicata dalla macchina dopo aver fatto il bilanciamento del bianco.
Se cambiamo tipo di illuminazione e facciamo un bilanciamento del bianco con la fotocamera, in pratica cambiamo le tre curve del bilanciamento appena viste, ma applichiamo lo stesso profilo ricavato in una diversa situazione di illuminazione, per cui non avremo una fedeltà assoluta dei colori, soprattutto se il profilo non è molto accurato,essendo calcolato a run-time dal processore della macchina, che approssima un po' per velocizzare il tempo di elaborazione. Memorizzare nella macchina fotografica le varie impostazioni di bilanciamento del bianco standard (Sole, Nuvole, Flash, Tungsteno ecc) significa memorizzare solo i punti del grigio relativi a questi illuminanti (quindi solo tre numeri con cui ricavare le curve, ovvero, nell'esempio sopra, 206,255,232 ), non significa riscrivere i profili ricavati nelle varie situazioni di illuminazione. Per questo i colori ottenuti non saranno ultra accurati. Invece, se vogliamo avere a disposizione un altro profilo per le nostre foto, tipo Adobe RGB, deve cambiare l'intera la tabella che lo rappresenta dentro alla macchina, o l'algoritmo che la ricostruisce. E' per questo che il numero di profili a disposizione è limitato a due o tre. In genere i profili memorizzati non sono Profili ICC, ma sono semplici algoritmi di conversione, che concettualmente funzionano in modo simile alla conversione fra profili ICC a matrice, e non sono molto accurati.
Camera Raw funziona in modo analogo, ma è molto più versatile. Anche Camera Raw associa dei profili ad ogni macchina fotografica, leggendo nei metadati del file raw il modello specifico. Per ogni fotocamera, Camera Raw memorizza due diversi profili. Uno creato per l'illuminante D65 (6500°K) e uno per l'illuminante A (2856°K). Il profilo effetivamente utilizzato, viene interpolato fra i due memorizzati, a seconda della temperatura di colore della scena. Tale informazione può essere il punto del bianco letto dalla macchina, se nelle impostazioni di White Balance lasciamo "As Shot", oppure possiamo settare manualmente la temperatura intervenendo sui cursori "Temperature" e "Tint", oppure possiamo fare un bilanciamento manuale usando lo strumento contagocce su una zona neutra della scena
I due profili associati alla fotocamera, dunque, cambiano da modello a modello, ma anche due esemplari dello stesso modello potrebbero essere caratterizzati da profili leggermente diversi, per motivi di tolleranze di fabbricazione. Con Camera Raw è possibile calibrarli in modo fine con i controlli nella pagina "Calibrate":
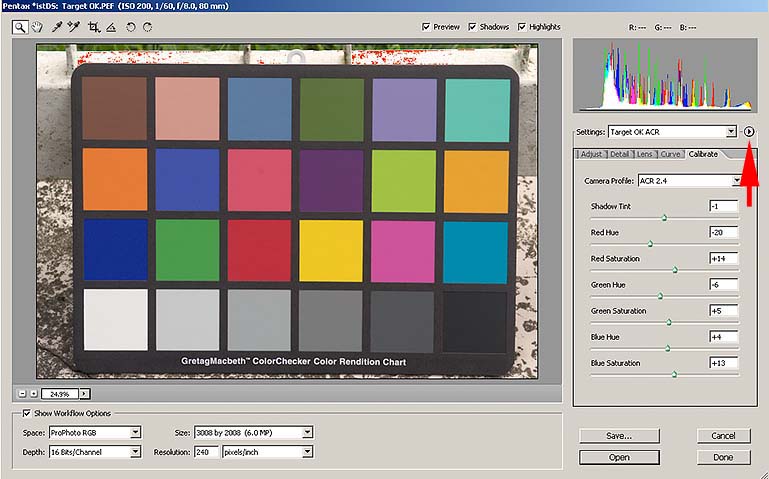
E c'è anche di più: se nel pulsantino indicato dalla freccia impostiamo "Save New Camera Raw Default", Camera Raw si ricorderà queste correzioni per questa particolare macchina digitale, itentificandola univocamente con il numero di serie che legge sempre nei metadati dei files raw.
Ma come si fa a regolare correttamente i parametri di questi profili? Lo si può fare a mano, provando e riprovando finchè i valori RGB delle 24 tacche non si avvicinano il più possibile a quelli reali, oppure si può utilizzare uno script java che lo fa per noi. Si chiama ACR Calibrator , è gratuito e ovviamente gira dentro a Photoshop. Non fa altro che aprire innumerevoli volte un file raw di una foto della testchart, e variando ogni volta un po' i parametri, trova i valori ottimali con cui riprodurre fedelmente i 24 colori. Quando finisce crea un'immagine con i valori trovati, come questa qui sotto:

Nel mio caso ha impiegato 43 minuti e 44 secondi, che è sempre meno di quanto ci avrei messo io facendolo a mano. Vediamo i risultati:
Camera Raw + ACR Calibrator

E' sicuramente migliorato molto. In particolare, guardando l'ultima riga con le tacche grigie, si nota che il contrasto è quasi perfetto. Anche gli altri colori sono mediamente migliorati.
Quindi il modo corretto di lavorare con Camera Raw è quello di eseguire questo tipo di calibrazione almeno per le situazioni di ripresa più frequenti (luce naturale, set di posa ecc), e di correggere eventualmente le immagini in fase di apertura utilizzando solamente i comandi nella pagina "Adjust". Nel caso in cui sia necessaria una riproduzione dei colori molto fedele conviene sempre seguire questa procedura nel primo scatto di ogni sessione.
E ora torniamo a DCRaw. Se da linea di comando di Windows lanciamo: dcraw.exe otteniamo le opzioni disponibili:
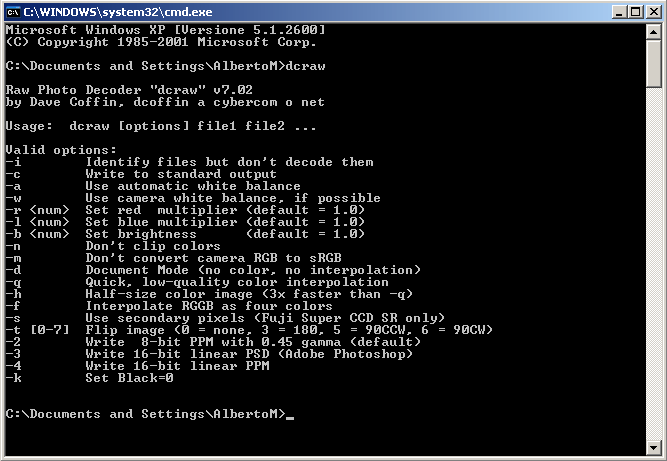
Se non esplicitiamo nessuna opzione, DCRaw converte nel formato ppm a 8 bit e in sRGB (non incorporato). La conversione più interessante, però è quella a 16 bit nel formato di Photoshop PSD. In questo modo i valori letti dalla fotocamera non vengono modificati con curve strane, ma vengono semplicemente trasformati da 12 a 16 bit, ovvero i valori letti internamente alla fotocamera risulteranno semplicemente moltiplicati per 216-12= 24 = 16 (per adesso supponiamo che sia proprio così, in realtà DCRaw funziona in modo un po' diverso, come è spiegato nel prossimo articolo). Un'immagine così convertita ha gamma circa uguale a 1, per cui se le assegnassimo il profilo sRGB, che ha gamma 2.2 la vedremmo sicuramente scura, come nell'esempio visto in un precedente articolo . La soluzione quindi è creare un profilo ICC apposito per la nostra fotocamera.
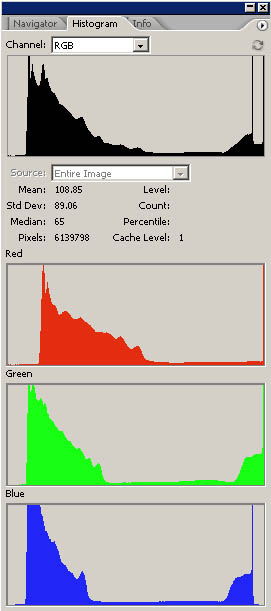
Però c'è un problema. Quando si converte nel formato PSD, DCRaw fa un'operazione che non dovrebbe fare, ovvero fa una specie di bilanciamento del punto del nero, che dipende dall'immagine che sta convertendo. Questa operazione è utile nella conversione a 8 bit, perchè produce colori più neutri e contrastati, ma nella conversione a 16 bit è solo dannosa, in quanto non permette una corretta gestione del colore tramite profili ICC. Mi spiego meglio con un esempio grafico:
 |
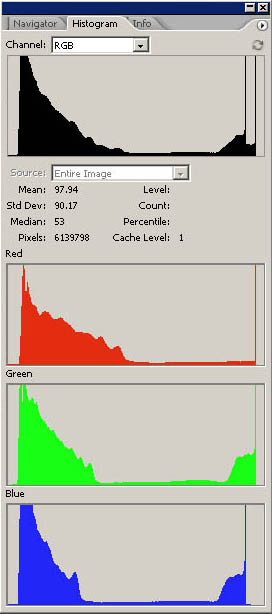 |
A sinistra abbiamo la conversione senza bilanciamento del nero, a destra quella che fa DCRaw. Vediamo che, praticamente, ha traslato i tre livelli RGB a sinistra, in modo da generare un punto del nero neutro, mentre nella conversione di sinistra il nero risultava più chiaro e sporcato da una dominante rossa. Quest'operazione sarebbe anche corretta, se non fosse per il fatto che non è costante per tutte le immagini, ma di volta in volta si calcola il valore ottimale da applicare e trasla i livelli in modo diverso. In questo modo un profilo ICC creato per un particolare scatto, non è applicabile ad altri scatti che possono avere compensazioni del nero diverse. Ho risolto questo problema andando a modificare leggermente il codice sorgente di DCRaw, che per fortuna è disponibile a tutti. Se notate fra le opzioni a disposizione nella riga di comando compare:
![]()
Questa opzione è una mia aggiunta, infatti non la trovate nelle versioni eseguibili di DCRaw che si trovano in giro per il web. Serve semplicemente ad evitare quella compensazione automatica del nero.
Occorre selezionare anche l'opzione -m , per evitare la conversione a sRGB. Tale conversione funziona solo se convertiamo ad 8 bit, mentre a 16 è solo un'inutile operazione che DCRaw fa di default senza realizzare una vera conversione a sRGB.
In definitiva, per convertire una serie di immagini raw il comando è:
dcraw -m -k -3 *.pef
(pef è il formato raw della Pentax)
Poi ho creato il profilo con ProfileMaker utilizzando il solito scatto della TestChart:
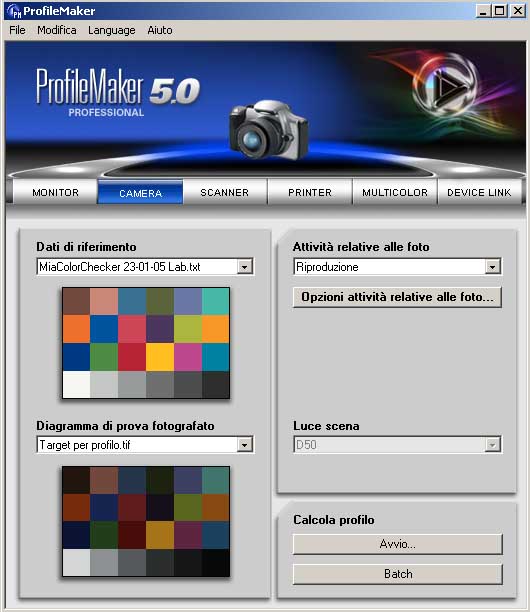
Poi , con Photoshop, ho assegnato il profilo creato e ho subito convertito a sRGB.
Vediamo come si presenta il target :
DCRaw + ProfileMaker

E'sicuramente la conversione meglio riuscita.
Se fotografiamo in condizioni d'illuminazione molto diverse conviene creare un profilo ad hoc . Quindi, anche in questo caso, il corretto modo di lavorare è creare dei profili per le situazioni di ripresa più frequenti (luce ambiente, flash ecc) ed eventualmente correggere le foto così convertite con gli strumenti di Photoshop, magari aiutandosi inserendo una testchart nella scena. Al solito, per una più accurata riproduzione dei colori è necessario crearsi un profilo per ogni sessione di scatti.
Osservazione: utilizzando questo metodo possiamo convertire la nostra immagine a qualunque spazio di lavoro, basta avere il profilo di destinazione. Con Camera Raw sono disponibili solo alcuni profili.
Vediamo ora uno scatto eseguito subito dopo quello della Testchart, nei quattro modi di conversione considerati:
JPEG

Camera Raw 3 Patches

Camera Raw + ACR Calibrator

DCRaw + ProfileMaker

In questo caso sappiamo che i colori più fedeli sono quelli dello scatto "DCRaw + Profilemaker", in quanto lo abbiamo potuto constatare direttamente sulla TestChart. Si può notare, però, che questa conversione risulta anche la meno contrastata. Nella fotografia di tutti i giorni una riproduzione molto fedele dei colori può apparire poco brillante e contrastata, quindi è facile ritrovarsi ad usare curve e saturazione per avvicinare di più l'immagine al proprio gusto personale. Per questo ProfileMaker mette a disposizione dei parametri di controllo in fase di creazione del profilo, volti appunto a "correggere" contrasto, saturazione, ecc per adattare il profilo ad un tipo particolare di ripresa, andando però a scapito della fedeltà dei colori. E' sempre per questo motivo che le fotocamere, quando scattano in JPEG, non rispettano i colori in modo troppo fedele, per non dare all'utente l'impressione di basso contrasto e poca vivacità dei colori, infatti si può notare che l'immagine JPEG è quella con i colori un po' più vivaci.
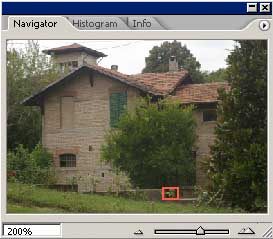
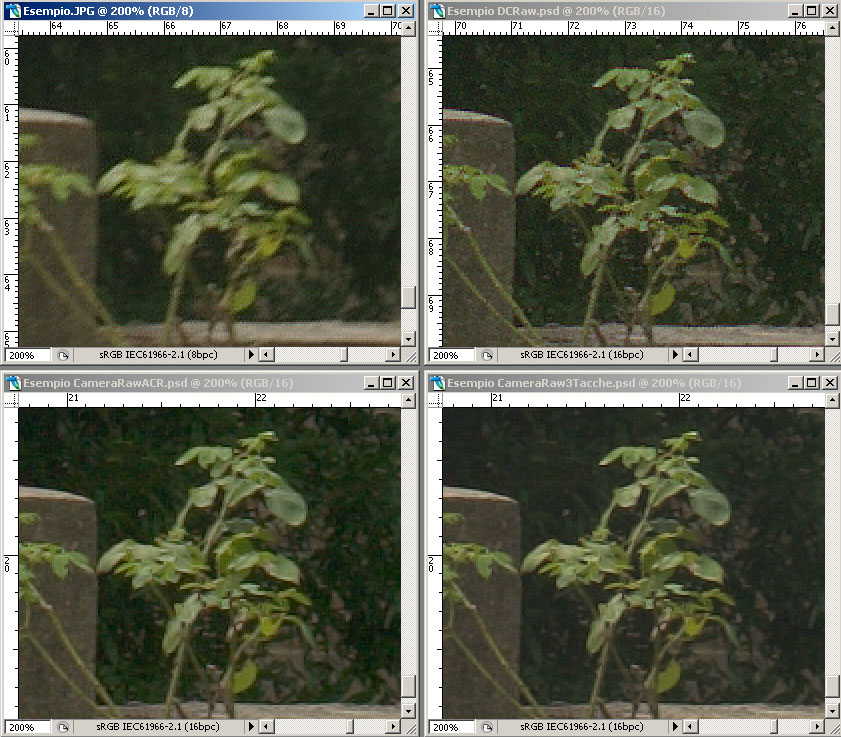
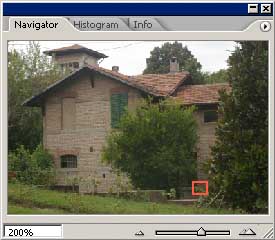
Ora vediamo la stessa immagine ingrandita al 200%. L'immagine JPEG è stata scattata utilizzando il valore più basso di Unsharp Mask impostabile sulla macchina. Successivamente è stato applicato con Photoshop CS2 un filtro di Smart Sharpen (quantità 250 e raggio 1) , mentre per le altre immagini è stato utilizzato il solito valore di 150 e raggio 0.8.
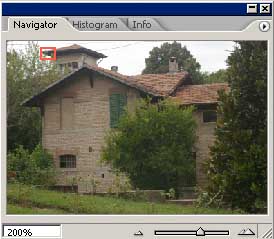 |
 |
 |
 |
 |
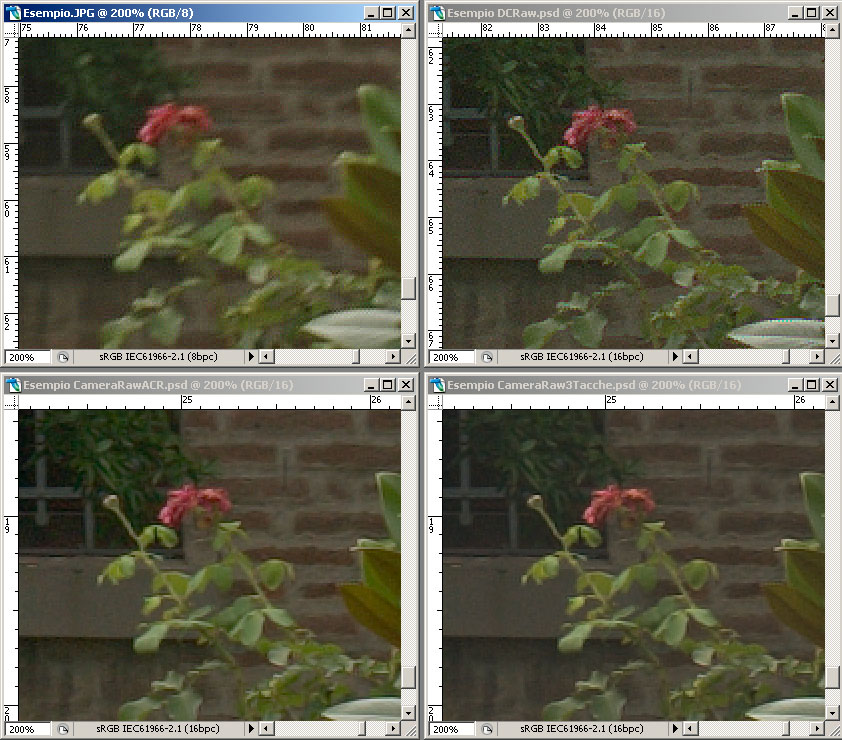 |
L'interpolazione fatta dalla macchina risulta decisamente scadente, inoltre si nota la compressione JPEG, in quanto il valore di Smart Sharpen applicato successivamente è elevato.
I colori relativi all'immagine convertita con DCRaw e a quella con Camera Raw+ACR Calibrator risultano molto simili, come ci si poteva aspettare.
Camera Raw applica di default una riduzione del rumore e dei fenomeni di color fringing che DCRaw non fa: lo si può fare a posteriori con filtri appositi.
In stampa un'immagine convertita con DCRaw appare più realistica perchè i dettagli sono meglio definiti, perchè in generale sono visibili meno artefatti (cristallizzazione) e perchè quella grana "elettronica" non corretta la rende più simile ad una foto chimica.
Osservazione: è possibile creare un profilo con ProfileMaker anche sulle immagini scattate in JPEG o convertite con Camera Raw, però nel primo caso si ha una perdita di qualità per la compressione a 8 bit del formato JPEG, nel secondo è un'operazione in più da fare: a quel punto conviene utilizzare direttamente DCRaw che fornisce risultati migliori nella resa dei dettagli.
Altra ossevazione: per creare il profilo di quest' articolo ho utilizzato una testchart a 24 tacche. Ne esistono in commercio di molto più adatte a questo scopo. Un esempio è la Colorchecker SG della GretagMacbeth che ha 140 tacche e quindi può creare profili molto più accurati.
Conclusione
Download
Qui potete scaricare la versione di DCRaw utilizzata nell'articolo (per Windows).
Non tutte le fotocamere sono supportate da questa versione, però è supportato il formato DNG della Adobe (Adobe Digital Negative) .
Per cui è possibile convertire, con il software Adobe, un qualunque formato raw al formato DNG senza perdita di informazione, e successivamente utilizzare DCRaw.
Aggiornamento 17/Sett/2005 . Ho aggiunto l'opzione -x spiegata nel prossimo articolo.
Qui invece trovate due profili creati rispettivamente per una Pentax *ist DS e per una Nikon D70.
Questi profili possono non essere perfetti per altri esemplari dello stesso modello, ma consentono comunque di provare DCRaw.